Advertisements
Advertisements
Question
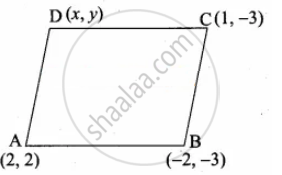
If the points A(2, 2), B(– 2, – 3), C(1, – 3) and D(x, y) form a parallelogram then find the value of x and y.
Solution
Let A(2, 2), B(– 2, – 3), C(1, – 3) and D(x, y) are the vertices of a parallelogram.
Slope of a line = `(y_2 - y_1)/(x_2 - x_1)`
Slope of AB = `(-3 - 2)/(-2 - 2) = (-5)/(-4) = 5/4`
Slope of BC = `(-3 + 3)/(-2 - 1) = 0/(-3)` = 0
Slope of CD = `(y + 3)/(x - 1)`
Slope of AD = `(y - 2)/(x - 2)`
Since ABCD is a parallelogram
Slope of AB = Slope of CD
`5/4 = (y + 3)/(x - 1)`
5(x – 1) = 4 (y + 3)
5x – 5 = 4y + 12
5x – 4y = 12 + 5
5x – 4y = 17 ...(1)
Slope of BC = Slope of AD
0 = `(y - 2)/(x - 2)`
y – 2 = 0
y = 2
Substitute the value of y = 2 in (1)
5x – 4(2) = 17
5x – 8 = 17
⇒ 5x = 17 + 8
5x = 25
⇒ x = `25/5` = 5
The value of x = 5 and y = 2.
APPEARS IN
RELATED QUESTIONS
What is the slope of a line whose inclination with positive direction of x-axis is 90°
What is the slope of a line whose inclination with positive direction of x-axis is 0°
What is the inclination of a line whose slope is 0
Find the slope of a line joining the points
(sin θ, – cos θ) and (– sin θ, cos θ)
Show that the given points are collinear: (– 3, – 4), (7, 2) and (12, 5)
The line through the points (– 2, a) and (9, 3) has slope `-1/2` Find the value of a.
Show that the given points form a parallelogram:
A(2.5, 3.5), B(10, – 4), C(2.5, – 2.5) and D(– 5, 5)
Let A(3, – 4), B(9, – 4), C(5, – 7) and D(7, – 7). Show that ABCD is a trapezium.
The slope of the line which is perpendicular to a line joining the points (0, 0) and (− 8, 8) is
If slope of the line PQ is `1/sqrt(3)` then slope of the perpendicular bisector of PQ is
