Advertisements
Advertisements
Question
Show that the given points form a parallelogram:
A(2.5, 3.5), B(10, – 4), C(2.5, – 2.5) and D(– 5, 5)
Solution
Let A(2.5, 3.5), B(10, – 4), C(2.5, – 2.5) and D(– 5, 5) are the vertices of a parallelogram.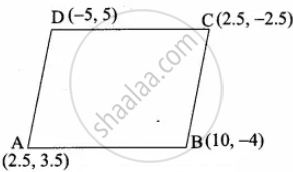
Slope of a line = `(y_2 - y_1)/(x_2 - x_1)`
Slope of AB = `(-4 - 3.5)/(10 - 2.5) = (-7.5)/(7.5)` = – 1
Slope of CD = `(5 + 2.5)/(-5 - 2.5) = (7.5)/(-7.5)` = – 1
Slope of AB = Slope of CD = – 1
∴ AB is Parallel to CD ...(1)
Slope of BC = `(-4 + 2.5)/(10 - 2.5) = (-1.5)/(7.5) = (-15)/75 = -1/5`
Slope of AD = `(5 - 3.5)/(-5 - 2.5) = 1.5/-7.5 = 15/(-75) = -1/5`
Slope of BC = Slope of AD
∴ BC is parallel to AD
From (1) and (2) we get ABCD is a parallelogram.
APPEARS IN
RELATED QUESTIONS
What is the slope of a line whose inclination with positive direction of x-axis is 90°
What is the inclination of a line whose slope is 0
What is the inclination of a line whose slope is 1
Find the slope of a line joining the points
`(5, sqrt(5))` with the origin
What is the slope of a line perpendicular to the line joining A(5, 1) and P where P is the mid-point of the segment joining (4, 2) and (–6, 4).
Show that the given points are collinear: (– 3, – 4), (7, 2) and (12, 5)
If the three points (3, – 1), (a, 3) and (1, – 3) are collinear, find the value of a
The line through the points (– 2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x.
The slope of the line joining (12, 3), (4, a) is `1/8`. The value of ‘a’ is
The slope of the line which is perpendicular to a line joining the points (0, 0) and (− 8, 8) is
