Advertisements
Advertisements
Question
If x + 2 is a factor of x2 + ax + 2b and a + b = 4, then
Options
a= 1, b = 3
a = 3, b = 1
a = −1, b = 5
a = 5, b = −1
Solution
Given that x + 2 is a factor of `x^2 + ax + 2b` and a + b=4
`f(x)=x ^2 +ax + 2b`
`f(-2)= (-2)^2 +a(-2 )+ 2b`
`0 = 4-2a +2b`
`-4 = -2a+2b`
By solving `-4 = -2a+2b` and a + b = 4 by elimination method we get
Multiply `a+b =4`by 2 we get,
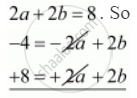
`4 = 4b`
`4/4=b`
By substituting b = 1 in a + b = 4 we get
`a+1 =4`
`a = 4-1`
`a =3`
Then a = 3, b = 1
Hence, the correct choice is `(b).`
APPEARS IN
RELATED QUESTIONS
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
`1/4 , -1`
If α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c, then evaluate α2β + αβ2
If α and β are the zeros of the quadratic polynomial f(x) = x2 − p (x + 1) — c, show that (α + 1)(β +1) = 1− c.
Find the zeroes of the quadratic polynomial f(x) = 4x2 - 4x - 3 and verify the relation between its zeroes and coefficients.
If p(x) = axr + bx + c, then –`"b"/"a"` is equal to ______.
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials:
3x2 + 4x – 4
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials:
t3 – 2t2 – 15t
Given that the zeroes of the cubic polynomial x3 – 6x2 + 3x + 10 are of the form a, a + b, a + 2b for some real numbers a and b, find the values of a and b as well as the zeroes of the given polynomial.
If α and β are the zeros of a polynomial f(x) = px2 – 2x + 3p and α + β = αβ, then p is ______.
If α, β are the zeroes of the polynomial p(x) = 4x2 – 3x – 7, then `(1/α + 1/β)` is equal to ______.
