Advertisements
Advertisements
Question
If `x = (sqrt(a + 3b) + sqrt(a - 3b))/(sqrt(a + 3b) - sqrt(a - 3b))`, prove that: 3bx2 – 2ax + 3b = 0.
Solution
`x = (sqrt(a + 3b) + sqrt(a - 3b))/(sqrt(a + 3b) - sqrt(a - 3b))`
Applying componendo and dividendo, we get,
`(x + 1)/(x - 1) = (sqrt(a + 3b) + sqrt(a - 3b) + sqrt(a + 3b) - sqrt(a - 3b))/(sqrt(a + 3b) + sqrt(a - 3b) - sqrt(a + 3b) + sqrt(a - 3b))`
`(x + 1)/(x - 1)= (2sqrt(a + 3b))/(2sqrt(a - 3b))`
Squaring both sides,
`(x^2 + 2x + 1)/(x^2 - 2x + 1) = (a + 3b)/(a - 3b)`
Again applying componendo and dividendo,
`(x^2 + 2x + 1 + x^2 - 2x + 1)/(x^2 + 2x + 1 - x^2 + 2x - 1) = (a + 3b + a - 3b)/(a + 3b - a + 3b)`
`(2(x^2 + 1))/(2(2x)) = (2(a))/(2(3b))`
3b(x2 + 1) = 2ax
3bx2 + 3b = 2ax
3bx2 – 2ax + 3b = 0
APPEARS IN
RELATED QUESTIONS
If q is the mean proportional between p and r, show that: pqr(p + q + r)3 = (pq + qr + rp)3.
Find the fourth proportional to 2xy, x2 and y2.
Find the mean proportion of the following :
24 and 6
Find the smallest number that must be subtracted from each of the numbers 20, 29, 84 and 129 so that they are in proportion.
Find the fourth proportional to 3, 12, 15
Find the fourth proportional to 1.5, 2.5, 4.5
An electric pole casts a shadow of length 20 m at a time when a tree 6 m high casts a shadow of length 8 m. Find the height of the pole.
Choose the correct answer from the given options :
The mean proportional between `(1)/(2)` and 128 is
Do the ratios 15 cm to 2 m and 10 sec to 3 minutes form a proportion?
Sleeping time of a python in a 24 hour clock is represented by the shaded portion in figure.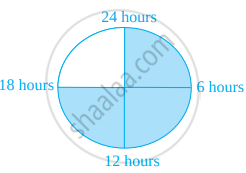
The ratio of sleeping time to awaking time is ______.
