Advertisements
Advertisements
Question
If the zeroes of the polynomial `f(x) = x^3 – 3x^2 + x + 1` are (a – b), a and (a + b), find the values of a and b.
Solution
By using the relationship between the zeroes of he quadratic polynomial.
We have, Sum of zeroes=`(-("Coefficient of" x^2))/("Coefficient of" x^3)`
∴ a – b + a + a + b=`-(-3)/1`
⇒ 3a = 3
⇒ a = 1
Now, Product of zeroes=`(-"(Constant term")/("Coefficient of" x^3)`
∴ (a – b) (a) (a + b)=`(-1)/1`
⇒ (1 – b) (1) (1 + b) = –1 [∵a =1]
⇒` 1 – b^2 = –1`
`⇒ b^2 = 2`
`⇒ b=+-sqrt2`
APPEARS IN
RELATED QUESTIONS
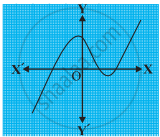
The graphs of y = p(x) are given in following figure, for some polynomials p(x). Find the number of zeroes of p(x).
Find the zeros of the polynomial `f(x) = x^2 + 7x + 12` and verify the relation between its zeroes and coefficients.
If f(x) =`x^3-3x+5x-3` is divided by g(x)=`x^2-2`
Find all the zeroes of `(2x^4 – 3x^3 – 5x2 + 9x – 3)`, it is being given that two of its zeroes are `sqrt3 and –sqrt3`.
Obtain all other zeroes of `(x^4 + 4x^3 – 2x^2 – 20x – 15)` if two of its zeroes are `sqrt5 and –sqrt5.`
Find the zeroes of the polynomial `x^2 – 3x – m(m + 3)`
If the zeroes of the quadratic polynomial x2 + (a + 1) x + b are 2 and –3, then ______.
Consider the following statements.
- x – 2 is a factor of x3 – 3x² + 4x – 4.
- x + 1 is a factor of 2x3 + 4x + 6.
- x – 1 is a factor of x5 + x4 – x3 + x² -x + 1.
In these statements
The zeroes of the quadratic polynomial x2 + kx + k, k ≠ 0 ______.
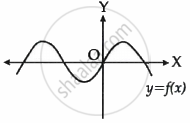
The graph of y = f(x) is shown in the figure for some polynomial f(x). The number of zeroes of f(x) are ______.