Advertisements
Advertisements
Question
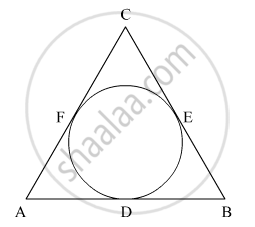
In Fig. 2, a circle is inscribed in a ΔABC, such that it touches the sides AB, BC and CA at points D, E and F respectively. If the lengths of sides AB, BC and CA and 12 cm, 8 cm and 10 cm respectively, find the lengths of AD, BE and CF.
Solution
t is given that
AB = 12 cm
⇒ AD + BD = 12 cm .....(1)
BC = 8 cm
⇒ BE + CE = 8 cm .....(2)
CA = 10 cm
⇒ AF + CF = 10 cm .....(3)
CF and CE act as tangents to the circle from the external point C.
It is known that the lengths of tangents drawn from an external point to a circle are equal.
∴ CF = CE .....(4)
Similarly, AF and AD act as tangents to the circle from the external point A
∴ AF = AD .....(5)
Also, BD and BE act as tangents to the circle from the external point B.
∴ BD = BE .....(6)
Using (4) and (2), we get
BE + CF = 8 cm .....(7)
Using (5) and (3), we get
AD + CF = 10 cm .....(8)
Using (6) and (1), we get
AD + BE = 12 cm .....(9)
Adding (7), (8) and (9), we get
BE + CF + AD + CF + AD + BE = 8 cm + 10 cm + 12 cm
⇒ 2AD + 2BE + 2CF = 30 cm
⇒ 2(AD + BE + CF) = 30 cm
⇒ AD + BE + CF = 15 cm .....(10)
Subtracting (7) from (10), we get
AD + BE + CF − BE − CF = 15 cm − 8 cm
⇒ AD = 7 cm
Subtracting (8) from (10), we get
AD + BE + CF − AD − CF = 15 cm − 10 cm
⇒ BE = 5 cm
Subtracting (9) from (10), we get
AD + BE + CF − AD − BE = 15 cm − 12 cm
⇒ CF = 3 cm
Thus, the lengths of AD, BE and CF are 7 cm, 5 cm and 3 cm, respectively.
APPEARS IN
RELATED QUESTIONS
Find the circumference and area of circle of radius 4.2 cm
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Circumference of the circle
Find the perimeter of a semicircular protractor whose diameter is 14 cm.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular cardboard of dimensions 14 cm ⨯ 7 cm. Find the area of the remaining cardboard.
A canvas tent is in the shape of a cylinder surmounted by a conical roof. The common diameter of the cone and the cylinder is 14 m. The height of the cylindrical part is 8 m and the height of the conical roof is 4 m. Find the area of the canvas used to make the tent.
The diameter of a right circular cylinder is 12 m and the slant height is 10 m. Find its curved surface area and the total surface area .
Find the total surface area and volume of a hemisphere whose radius is 10 cm.
The diameter of a circle is 28 cm.
Find its :
(i) Circumference
(ii) Area.
Ratio of circumference of a circle to its radius is always 2π:I.
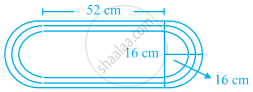
Ishika has designed a small oval race track for her remote control car. Her design is shown in the given figure. What is the total distance around the track? Round your answer to the nearest whole centimetre.