Advertisements
Advertisements
Question
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
Solution

The equations of the planes are 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
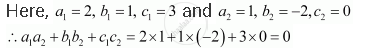
Thus, the given planes are perpendicular to each other.
APPEARS IN
RELATED QUESTIONS
Find the angle between the planes `bar r.(2bar i+barj-bark)=3 and bar r.(hati+2hatj+hatk)=1`
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
4x + 8y + z – 8 = 0 and y + z – 4 = 0
Find the angle between the given planes. \[\vec{r} \cdot \left( 2 \hat{i} - 3 \hat{j} + 4 \hat{k} \right) = 1 \text{ and } \vec{r} \cdot \left( - \hat{i} + \hat{j} \right) = 4\]
Find the angle between the given planes. \[\vec{r} \cdot \left( 2 \hat{i} - \hat{j} + 2 \hat{k} \right) = 6 \text{ and } \vec{r} \cdot \left( 3 \hat{i} + 6 \hat{j} - 2 \hat{k} \right) = 9\]
Find the angle between the planes.
2x − y + z = 4 and x + y + 2z = 3
Find the angle between the planes.
x + y − 2z = 3 and 2x − 2y + z = 5
Find the angle between the planes.
x − y + z = 5 and x + 2y + z = 9
Find the angle between the planes.
2x − 3y + 4z = 1 and − x + y = 4
Show that the following planes are at right angles.
\[\vec{r} \cdot \left( 2 \hat{i} - \hat{j} + \hat{k} \right) = 5 \text{ and } \vec{r} \cdot \left( - \hat{i} - \hat{j} + \hat{k} \right) = 3\]
Show that the following planes are at right angles.
x − 2y + 4z = 10 and 18x + 17y + 4z = 49
The acute angle between the planes 2x − y + z = 6 and x + y + 2z = 3 is
The acute angle between the two planes x+y+2z = 3 and 3x -2y +2z = 7 ________.
The function `f(x) = log(1 + x) - (2x)/(2 + x)` is increasing on
A block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10 N, the mass of the block (in kg) is (take g = 10 m/s2)
