Advertisements
Advertisements
Question
In a huge park people are concentrated at three points (see the given figure):

A: where there are different slides and swings for children,
B: near which a man-made lake is situated,
C: which is near to a large parking and exit.
Where should an ice-cream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlor should be equidistant from A, B and C)
Solution
Maximum number of persons can approach the ice-cream parlour if it is equidistant from A, B and C. Now, A, B and C form a triangle. In a triangle, the circumcentre is the only point that is equidistant from its vertices. So, the ice-cream parlour should be set up at the circumcentre O of ΔABC.
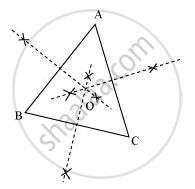
In this situation, maximum number of persons can approach it. We can find circumcentre O of this triangle by drawing perpendicular bisectors of the sides of this triangle.
APPEARS IN
RELATED QUESTIONS
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

From the following figure, prove that: AB > CD.
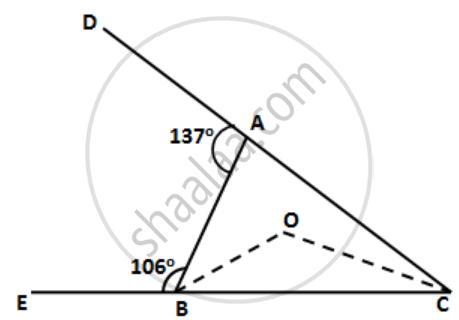
Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.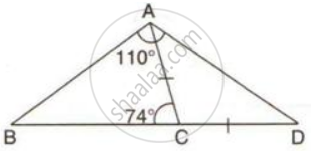
Prove that: BC > CD.
In the following figure, write BC, AC, and CD in ascending order of their lengths.
"Issues of caste discrimination began to be written about in many printed tracts and essays in India in the late nineteenth century." Support the statement with two suitable examples.
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
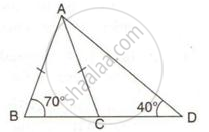
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.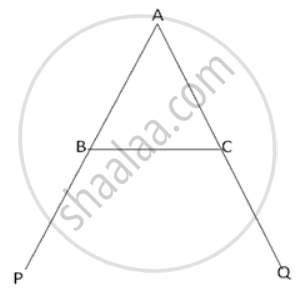
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR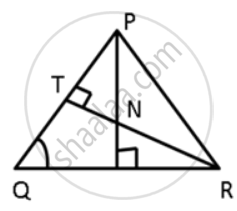
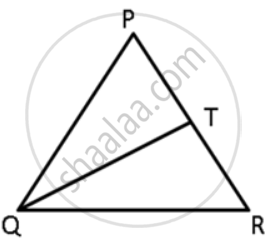
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT