Advertisements
Advertisements
Question
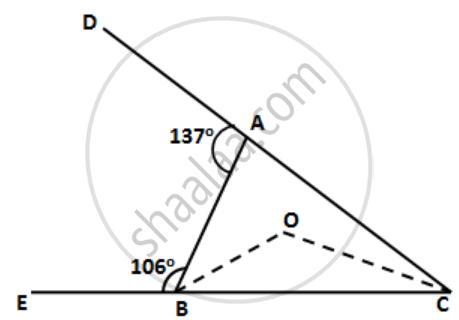
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.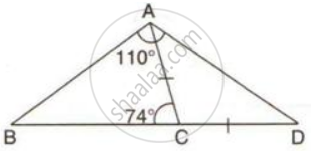
Prove that: BC > CD.
Solution
∠ACB = 74° ...(i)[ Given ]
∠ACB + ∠ACD = 180° ....[ BCD is a straight line ]
⇒ 74° + ∠ACD = 180°
⇒ ∠ACD = 106° …..(ii)
In ΔACD,
∠ACD + ∠ADC+ ∠CAD = 180°
Given that AC = CD
⇒ ∠ADC= ∠CAD
⇒ 106° + ∠CAD + ∠CAD = 180° ....[From (ii)]
⇒ 2∠CAD = 74°
⇒ ∠CAD = 37° = ∠ADC ...(iii)
Now,
∠BAD = 110° ....[Given]
∠BAC + ∠CAD = 110°
∠BAC + 37° = 110°
∠ BAC = 73° ….(iv)
In ABC,
∠ B + ∠BAC + ∠ACB = 180°
∠B + 73° + 74° = 180° ...[From (i) and (iv)]
∠B + 147°= 180°
∠B = 33° …..(v)
∴ ∠BAC > ∠B ...[ From (iv) and (v)]
⇒ BC > AC
But,
AC = CD ...[ Given ]
⇒ BC > CD
APPEARS IN
RELATED QUESTIONS
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
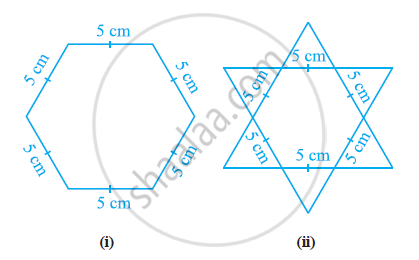
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
In the following figure, write BC, AC, and CD in ascending order of their lengths.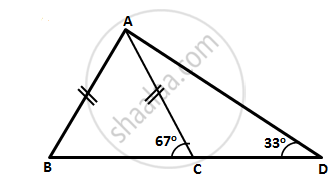
Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
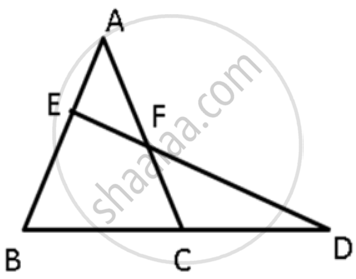
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
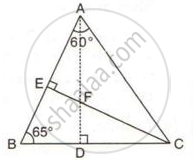
Prove that:
(i) CF > AF
(ii) DC > DF
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).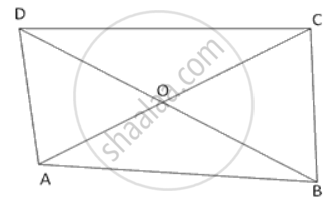
ABCD is a trapezium. Prove that: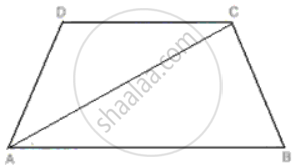
CD + DA + AB + BC > 2AC.
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.