Advertisements
Advertisements
प्रश्न
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.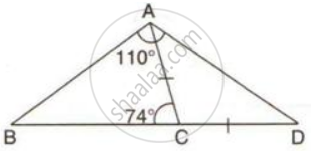
Prove that: BC > CD.
उत्तर
∠ACB = 74° ...(i)[ Given ]
∠ACB + ∠ACD = 180° ....[ BCD is a straight line ]
⇒ 74° + ∠ACD = 180°
⇒ ∠ACD = 106° …..(ii)
In ΔACD,
∠ACD + ∠ADC+ ∠CAD = 180°
Given that AC = CD
⇒ ∠ADC= ∠CAD
⇒ 106° + ∠CAD + ∠CAD = 180° ....[From (ii)]
⇒ 2∠CAD = 74°
⇒ ∠CAD = 37° = ∠ADC ...(iii)
Now,
∠BAD = 110° ....[Given]
∠BAC + ∠CAD = 110°
∠BAC + 37° = 110°
∠ BAC = 73° ….(iv)
In ABC,
∠ B + ∠BAC + ∠ACB = 180°
∠B + 73° + 74° = 180° ...[From (i) and (iv)]
∠B + 147°= 180°
∠B = 33° …..(v)
∴ ∠BAC > ∠B ...[ From (iv) and (v)]
⇒ BC > AC
But,
AC = CD ...[ Given ]
⇒ BC > CD
APPEARS IN
संबंधित प्रश्न
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
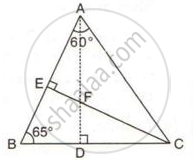
Prove that:
(i) CF > AF
(ii) DC > DF
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?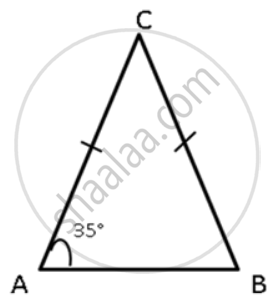
Prove that the perimeter of a triangle is greater than the sum of its three medians.
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS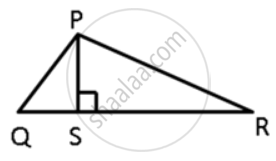
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT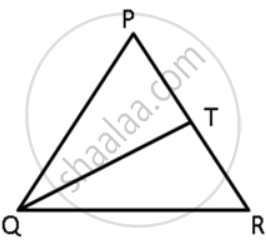
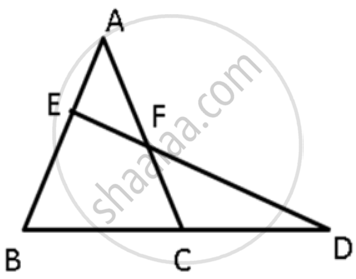
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.