Advertisements
Advertisements
प्रश्न
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT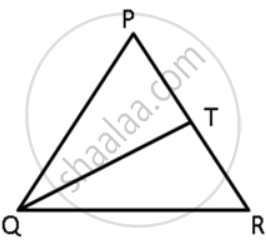
उत्तर
In ΔPQR,
PQ = QR = PR
⇒ ∠P = Q = ∠ = 60°
In ΔTQR,
∠TQR < 60°
∴ ∠TQR < ∠R
∴ RT < QT.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
Prove that the perimeter of a triangle is greater than the sum of its three medians.
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN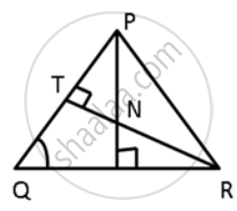
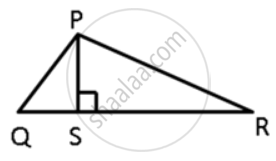
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS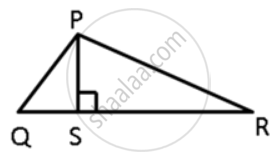
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS