Advertisements
Advertisements
Question
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT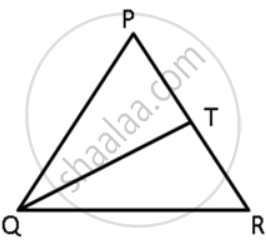
Solution
In ΔPQR,
PQ = QR = PR
⇒ ∠P = Q = ∠ = 60°
In ΔTQR,
∠TQR < 60°
∴ ∠TQR < ∠R
∴ RT < QT.
APPEARS IN
RELATED QUESTIONS
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
In a huge park people are concentrated at three points (see the given figure):

A: where there are different slides and swings for children,
B: near which a man-made lake is situated,
C: which is near to a large parking and exit.
Where should an ice-cream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlor should be equidistant from A, B and C)
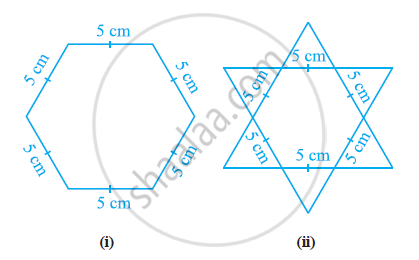
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?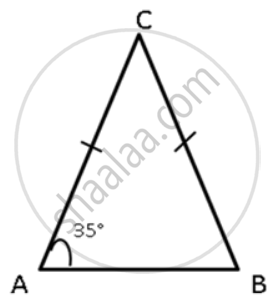
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR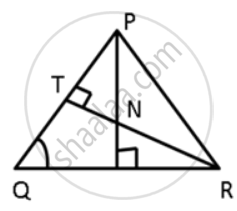
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.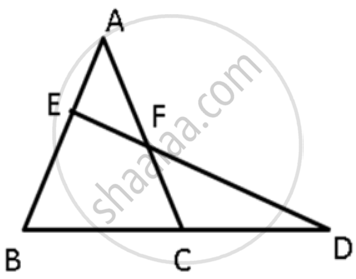
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
