Advertisements
Advertisements
Question
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
Solution

In the ΔABC,
AB + AC > BC .....(∵ Sum of the two sides of triangle is always greater than third side.) ....(i)
Also, in the ΔBDC,
BD + DC > BC ....(ii)
Dividing (i) by (ii),
`"AB + AC"/"BD + DC" > "BC"/"BC"`
`"AB + AC"/"BD + DC" > 1`
AB + AC > BD + DC
i.e. BD + DC < AB + AC.
APPEARS IN
RELATED QUESTIONS
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
Prove that the hypotenuse is the longest side in a right-angled triangle.
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN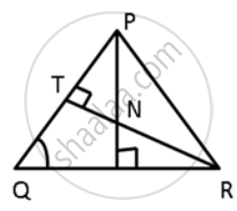
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.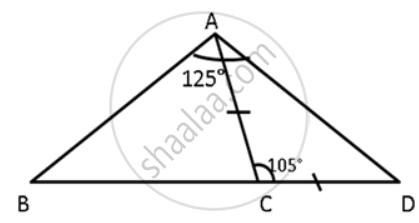
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT