Advertisements
Advertisements
Question
Prove that the hypotenuse is the longest side in a right-angled triangle.
Solution
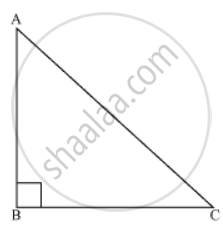
Let us consider a right angled triangle ABC, right angle at B.
In ΔABC
∠A + ∠B +∠C = 180° ...(angle sum property of a triangle)
∠A + 90° + ∠C = 180°
∠A +∠C = 90°
Hence, the other two angles have to be acute (i.e. less than 90°).
∴ ∠B is the largest angle in ΔABC.
⇒ ∠B > ∠A and ∠B > ∠C
⇒ AC > BC and AC > AB
[In ant triangle, the side opposite to the larger (greater) angle is longer]
So, Ac is the largest side in ΔABC.
But AC is the hypotenuse of ΔABC. Therefore, hypotenuse is the longest side in a right angled triangle.
APPEARS IN
RELATED QUESTIONS
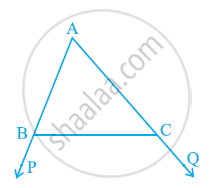
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
In the following figure, write BC, AC, and CD in ascending order of their lengths.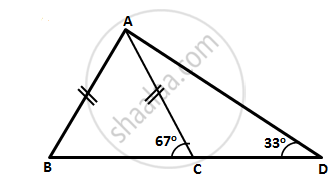
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
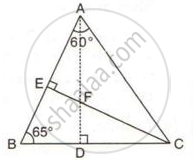
Prove that:
(i) CF > AF
(ii) DC > DF
"Caste inequalities are still prevalent in India." Examine the statement.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.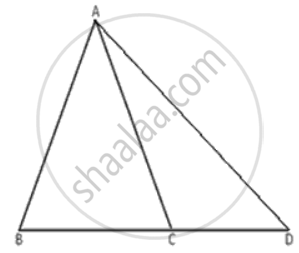
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT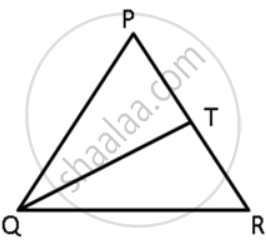
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
