Advertisements
Advertisements
Question
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
Solution
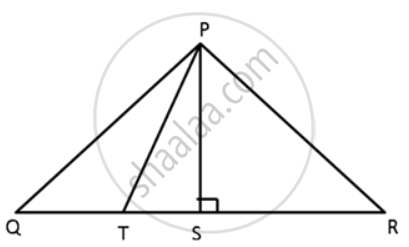
Let the triangle be PQR.
PS QR, the straight line joining vertex P
to the line QR.
To prove : PQ > PT and PR > PT
In ΔPSQ,
PS2 + SQ2 = PQ2 ....(Pythagoras theroem)
PS2 = PQ2 - SQ2 ....(i)
In ΔPST,
PS2 + ST2 = PT2 ....(Pythagoras theroem)
PQ2 - SQ2 = PT2 - ST2 ....(ii)
PQ - (ST + TQ)2 = PT2 - ST2 ....[from (i) and (ii)]
PQ2 - (ST2 - 2ST x TQ + TQ2) = PT2 - ST2
PQ2 - (ST2 - 2ST x TQ - TQ2 = PT2 - ST
PQ2 - PT2 = TQ2 + 2ST x TQ
PQ2 - PT2 = TQ x (2ST + TQ)
As, TQ x (2ST + TQ) > 0 always.
PQ2 - PT2 > 0
PQ2 > PT2
PQ > PT
Also, PQ = PR
PR > PT.
APPEARS IN
RELATED QUESTIONS
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.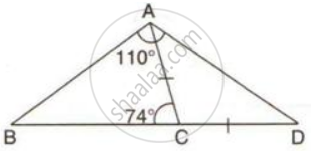
Prove that: BC > CD.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Arrange the sides of the following triangles in an ascending order:
ΔABC, ∠A = 45°, ∠B = 65°.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
ABCD is a trapezium. Prove that: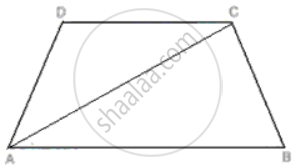
CD + DA + AB > BC.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR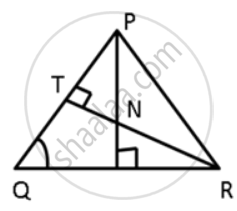
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS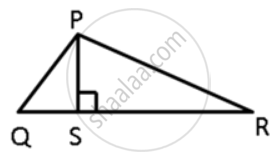
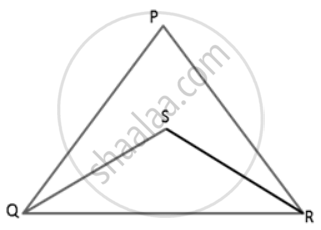
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.