Advertisements
Advertisements
प्रश्न
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
उत्तर
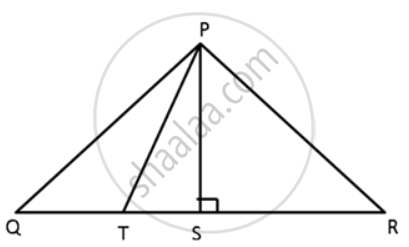
Let the triangle be PQR.
PS QR, the straight line joining vertex P
to the line QR.
To prove : PQ > PT and PR > PT
In ΔPSQ,
PS2 + SQ2 = PQ2 ....(Pythagoras theroem)
PS2 = PQ2 - SQ2 ....(i)
In ΔPST,
PS2 + ST2 = PT2 ....(Pythagoras theroem)
PQ2 - SQ2 = PT2 - ST2 ....(ii)
PQ - (ST + TQ)2 = PT2 - ST2 ....[from (i) and (ii)]
PQ2 - (ST2 - 2ST x TQ + TQ2) = PT2 - ST2
PQ2 - (ST2 - 2ST x TQ - TQ2 = PT2 - ST
PQ2 - PT2 = TQ2 + 2ST x TQ
PQ2 - PT2 = TQ x (2ST + TQ)
As, TQ x (2ST + TQ) > 0 always.
PQ2 - PT2 > 0
PQ2 > PT2
PQ > PT
Also, PQ = PR
PR > PT.
APPEARS IN
संबंधित प्रश्न
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
In the following figure, write BC, AC, and CD in ascending order of their lengths.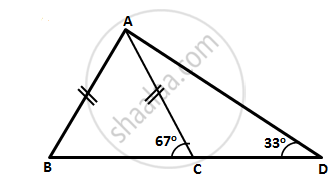
Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
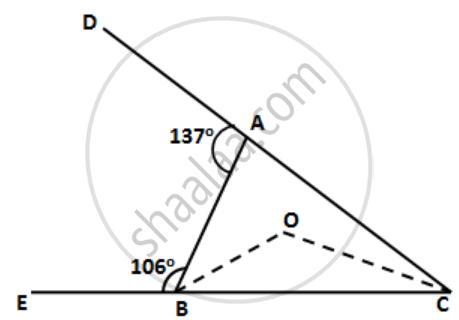
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.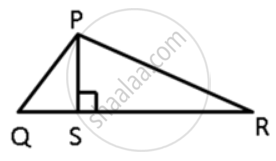
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT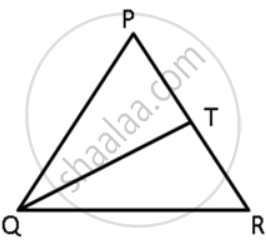
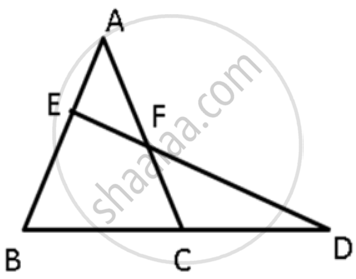
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.