Advertisements
Advertisements
प्रश्न
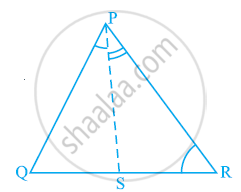
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
उत्तर
As PR > PQ,
∴ ∠PQR > ∠PRQ (Angle opposite to larger side is larger) ... (1)
PS is the bisector of ∠QPR.
∴∠QPS = ∠RPS ... (2)
∠PSR is the exterior angle of ΔPQS.
∴ ∠PSR = ∠PQR + ∠QPS ... (3)
∠PSQ is the exterior angle of ΔPRS.
∴ ∠PSQ = ∠PRQ + ∠RPS ... (4)
Adding equations (1) and (2), we obtain
∠PQR + ∠QPS > ∠PRQ + ∠RPS
⇒ ∠PSR > ∠PSQ [Using the values of equations (3) and (4)]
APPEARS IN
संबंधित प्रश्न
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
"Issues of caste discrimination began to be written about in many printed tracts and essays in India in the late nineteenth century." Support the statement with two suitable examples.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
Prove that the perimeter of a triangle is greater than the sum of its three medians.
ABCD is a trapezium. Prove that: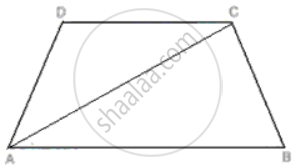
CD + DA + AB > BC.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR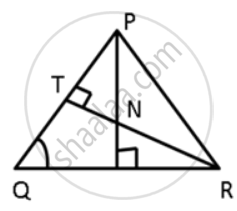
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS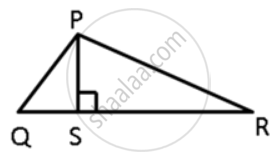
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
