Advertisements
Advertisements
प्रश्न
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

उत्तर
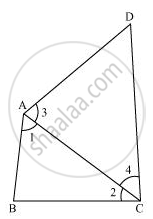
Let us join AC.
In ΔABC,
AB < BC (AB is the smallest side of quadrilateral ABCD)
∴ ∠2 < ∠1 (Angle opposite to the smaller side is smaller) ... (1)
In ΔADC,
AD < CD (CD is the largest side of quadrilateral ABCD)
∴ ∠4 < ∠3 (Angle opposite to the smaller side is smaller) ... (2)
On adding equations (1) and (2), we obtain
∠2 + ∠4 < ∠1 + ∠3
⇒ ∠C < ∠A
⇒ ∠A > ∠C
Let us join BD.

In ΔABD,
AB < AD (AB is the smallest side of quadrilateral ABCD)
∴ ∠8 < ∠5 (Angle opposite to the smaller side is smaller) ... (3)
In ΔBDC,
BC < CD (CD is the largest side of quadrilateral ABCD)
∴ ∠7 < ∠6 (Angle opposite to the smaller side is smaller) ... (4)
On adding equations (3) and (4), we obtain
∠8 + ∠7 < ∠5 + ∠6
⇒ ∠D < ∠B
⇒ ∠B > ∠D
APPEARS IN
संबंधित प्रश्न
How had the position of women improved in our country since independence ? Explain with examples.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
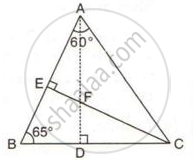
Prove that:
(i) CF > AF
(ii) DC > DF
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?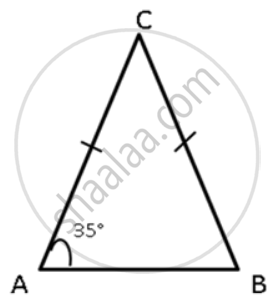
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).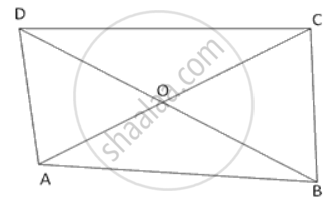
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN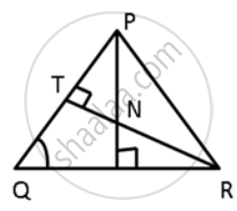
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.