Advertisements
Advertisements
प्रश्न
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

उत्तर
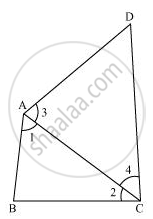
Let us join AC.
In ΔABC,
AB < BC (AB is the smallest side of quadrilateral ABCD)
∴ ∠2 < ∠1 (Angle opposite to the smaller side is smaller) ... (1)
In ΔADC,
AD < CD (CD is the largest side of quadrilateral ABCD)
∴ ∠4 < ∠3 (Angle opposite to the smaller side is smaller) ... (2)
On adding equations (1) and (2), we obtain
∠2 + ∠4 < ∠1 + ∠3
⇒ ∠C < ∠A
⇒ ∠A > ∠C
Let us join BD.

In ΔABD,
AB < AD (AB is the smallest side of quadrilateral ABCD)
∴ ∠8 < ∠5 (Angle opposite to the smaller side is smaller) ... (3)
In ΔBDC,
BC < CD (CD is the largest side of quadrilateral ABCD)
∴ ∠7 < ∠6 (Angle opposite to the smaller side is smaller) ... (4)
On adding equations (3) and (4), we obtain
∠8 + ∠7 < ∠5 + ∠6
⇒ ∠D < ∠B
⇒ ∠B > ∠D
APPEARS IN
संबंधित प्रश्न
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
"Caste inequalities are still prevalent in India." Examine the statement.
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
ABCD is a trapezium. Prove that: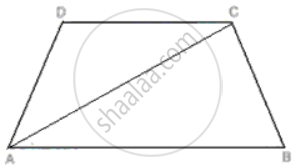
CD + DA + AB > BC.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR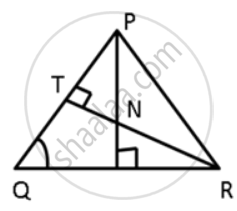
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS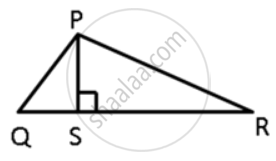
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.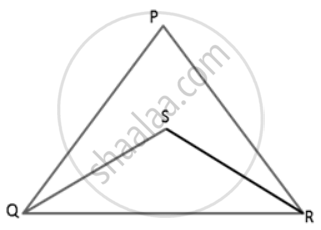
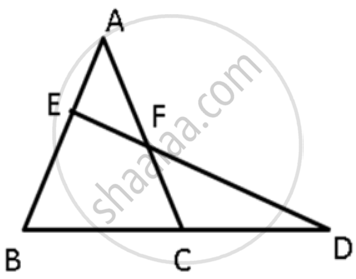
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.