Advertisements
Advertisements
प्रश्न
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.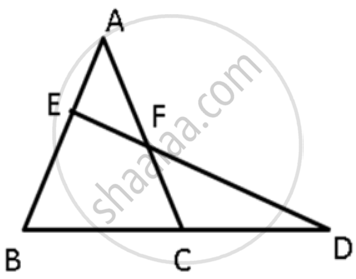
उत्तर
∠AEF > ∠ABC ...(Exterior angle property)
∠AEF = ∠DFC
∠ACB > ∠DFC ...(Exterior angle property)
⇒ ∠ACB > ∠AFE
Since AB = AC
⇒ ∠ACB = ∠ABC
So, ∠ABC > ∠AFE
⇒ ∠AEF > ∠ABC > ∠AFE
that is ∠AEF > ∠AFE
⇒ AF > AE.
APPEARS IN
संबंधित प्रश्न
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
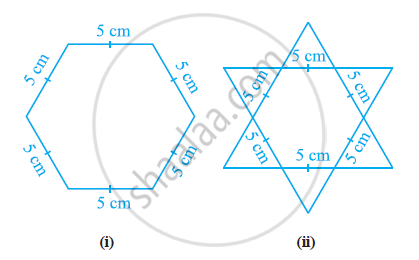
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
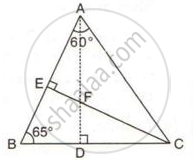
Prove that:
(i) CF > AF
(ii) DC > DF
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.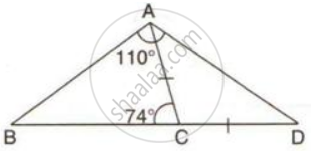
Prove that: BC > CD.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
ABCD is a trapezium. Prove that: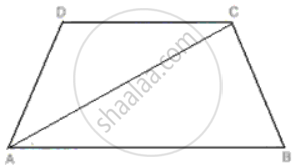
CD + DA + AB + BC > 2AC.
ABCD is a trapezium. Prove that: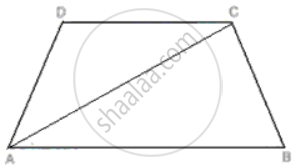
CD + DA + AB > BC.
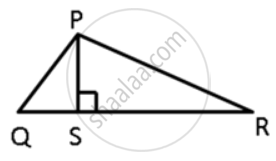
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS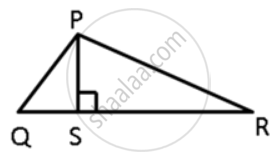
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS