Advertisements
Advertisements
प्रश्न
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
उत्तर
The point which is equidistant from all the sides of a triangle is called the incentre of the triangle. Incentre of a triangle is the intersection point of the angle bisectors of the interior angles of that triangle.
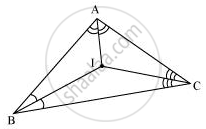
Here, in ΔABC, we can find the incentre of this triangle by drawing the angle bisectors of the interior angles of this triangle. I is the point where these angle bisectors are intersecting each other. Therefore, I is the point equidistant from all the sides of ΔABC.
APPEARS IN
संबंधित प्रश्न
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

In a huge park people are concentrated at three points (see the given figure):

A: where there are different slides and swings for children,
B: near which a man-made lake is situated,
C: which is near to a large parking and exit.
Where should an ice-cream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlor should be equidistant from A, B and C)
How had the position of women improved in our country since independence ? Explain with examples.
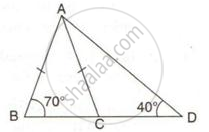
From the following figure, prove that: AB > CD.
"Issues of caste discrimination began to be written about in many printed tracts and essays in India in the late nineteenth century." Support the statement with two suitable examples.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the greatest and the smallest sides in the following triangles:
ΔXYZ, ∠X = 76°, ∠Y = 84°.
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
ABCD is a trapezium. Prove that: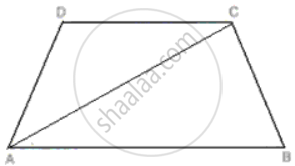
CD + DA + AB + BC > 2AC.
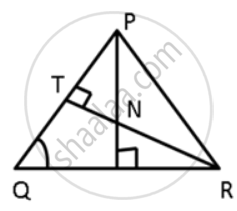
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN