Advertisements
Advertisements
प्रश्न
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
उत्तर
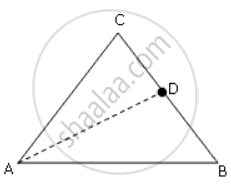
Construction: Join AD
In triangle ACD,
AC + CD > AD ...(i)
(Sum of two of a triangle greater than the third side)
Similarly, in triangle ADB,
AB + BD > AD ...(ii)
Adding (i) and (ii),
AC + CD + AB + BD > AD
AB + BC + AC > 2AD. ...(Since, CD + BD = BC)
APPEARS IN
संबंधित प्रश्न
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
From the following figure, prove that: AB > CD.
In the following figure, write BC, AC, and CD in ascending order of their lengths.
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
ABCD is a trapezium. Prove that: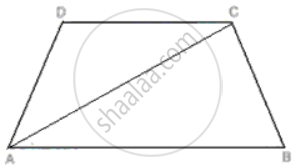
CD + DA + AB > BC.
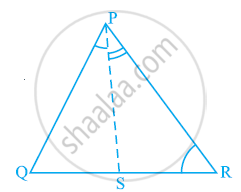
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN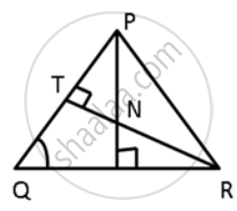
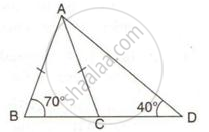
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.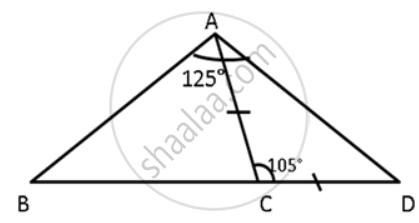
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.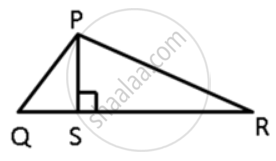
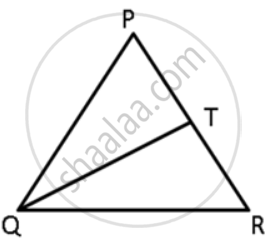
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT