Advertisements
Advertisements
प्रश्न
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
उत्तर
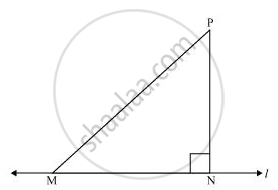
Let us take a line l and from point P (i.e., not on line l), draw two line segments PN and PM. Let PN be perpendicular to line l and PM is drawn at some other angle.
In ΔPNM,
∠N = 90º
∠P + ∠N + ∠M = 180º (Angle sum property of a triangle)
∠P + ∠M = 90º
Clearly, ∠M is an acute angle.
∴ ∠M < ∠N
⇒ PN < PM (Side opposite to the smaller angle is smaller)
Similarly, by drawing different line segments from P to l, it can be proved that PN is smaller in comparison to them.
Therefore, it can be observed that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
APPEARS IN
संबंधित प्रश्न
Show that in a right angled triangle, the hypotenuse is the longest side.
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?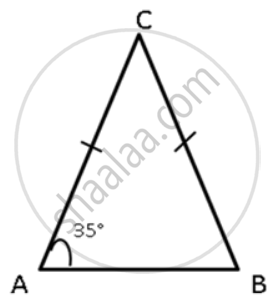
Prove that the perimeter of a triangle is greater than the sum of its three medians.
ABCD is a trapezium. Prove that: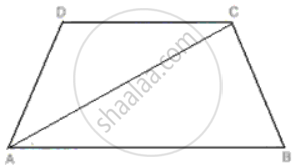
CD + DA + AB + BC > 2AC.
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS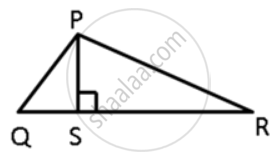
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
