Advertisements
Advertisements
प्रश्न
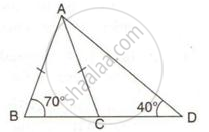
In the following figure, write BC, AC, and CD in ascending order of their lengths.
उत्तर

In ΔABC,
∠BAC < ∠ABC
BC < AC ....( 1 )
Now, ∠ACB = 180° - ∠ABC - ∠BAC
∠ACB = 180° - 73° - 47°
∠ACB = 60°
Now, ∠ACD = 180° - ∠ACB
∠ACD = 180° - 60° = 120°
Now, in ΔACD,
∠ADC = 180° - ∠ACD - ∠CAD
∠ADC = 180° - 120° - 31°
∠ADC = 29°
Since ∠ADC < ∠CAD, we have
AC < CD ....( 2 )
From ( 1 ) and ( 2 ), we have
BC < AC < CD.
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
From the following figure, prove that: AB > CD.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.