Advertisements
Advertisements
प्रश्न
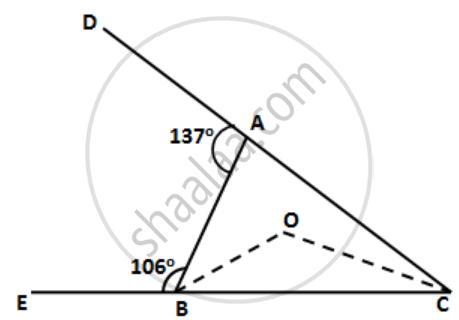
Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
उत्तर

∠BAC = 180° - ∠BAD = 180° - 137° = 43°
∠ABC = 180° - ∠ABE = 180° - 106° = 74°
Thus, in ΔABC,
∠ACB = 180° - ∠BAC - ∠ABC
⇒ ∠ACB = 180° - 43° - 74° = 63°
Now, ∠ABC = ∠OBC + ∠ABO
⇒ ∠ABC = 2∠OBC ....( OB is biosector of ∠ABC )
⇒ 74° = 2∠OBC
⇒ ∠OBC = 37°
Similarly,
∠ACB = ∠OCB + ∠ACO
⇒ ∠ACB = 2∠OCB ...( OC is bisector of ACB )
⇒ 63° = 2∠OCB
⇒ ∠OCB = 31.5°
Now, in ΔBOC,
∠BOC = 180° - ∠OBC - ∠OCB
⇒ ∠BOC = 180° - 37° - 31.5°
⇒ ∠BOC = 111.5°
Since, ∠BOC> ∠OBC > ∠OCB, we have
BC > OC > OB
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?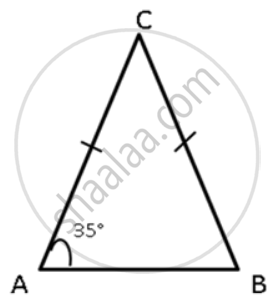
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.
Prove that the hypotenuse is the longest side in a right-angled triangle.
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR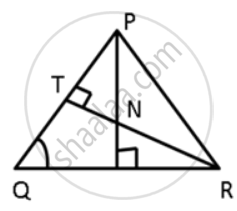
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS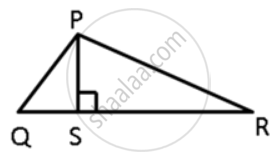
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.