Advertisements
Advertisements
प्रश्न
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
उत्तर
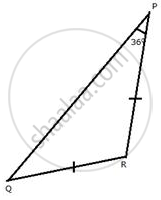
In ΔPQR,
QR = PR ...[ Given ]
∴ ∠P = ∠Q ...[ angles opposite to equal sides are equal ]
⇒ ∠P = 36° ..[Given]
⇒ ∠Q = 36°
In ΔPQR,
∠P + ∠Q + ∠R = 180°
⇒ 36° + 36° + ∠R = 180°
⇒ ∠R + 72° = 180°
⇒ ∠R = 108°
Now,
∠R = 108°
∠P = 36°
∠Q = 36°
Since ∠R is the greatest, therefore, PQ is the largest side.
APPEARS IN
संबंधित प्रश्न
Show that in a right angled triangle, the hypotenuse is the longest side.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
From the following figure, prove that: AB > CD.
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.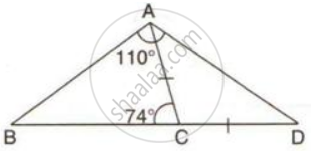
Prove that: BC > CD.
In the following figure, write BC, AC, and CD in ascending order of their lengths.
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.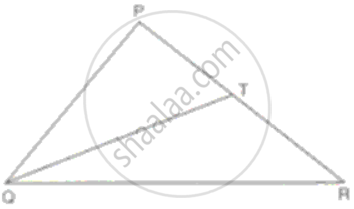
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR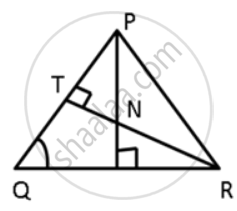
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.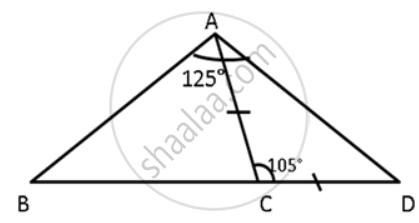
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.