Advertisements
Advertisements
प्रश्न
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.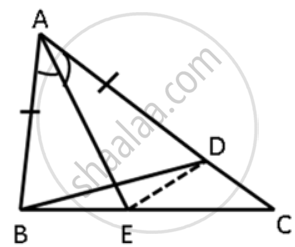
उत्तर
In the ΔABE and ΔADE,
AB = AD ....(Given)
∠BAE = ∠DAE ....(AE is the bisector of ∠BAC)
AE = AE ....(Common side)
∴ ΔABE ≅ ΔADE ....(SAS test)
⇒ BE = DE ....(c.p.c.t.c)
In ΔABD,
AB = AD
⇒ ∠ABD = ∠ADB
∠ADB > ∠C ...(Exterior angle property)
⇒ ∠ABD > ∠C.
APPEARS IN
संबंधित प्रश्न
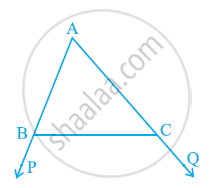
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
How had the position of women improved in our country since independence ? Explain with examples.
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
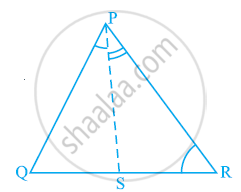
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR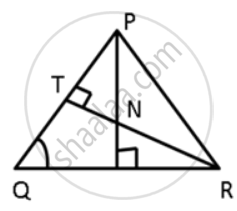
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.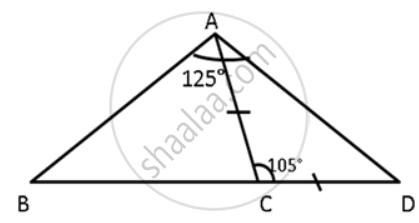
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT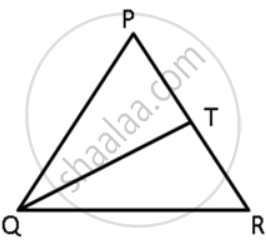
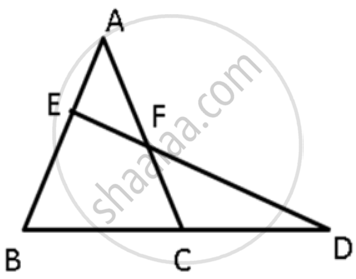
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.