Advertisements
Advertisements
प्रश्न
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
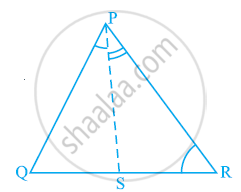
उत्तर
As PR > PQ,
∴ ∠PQR > ∠PRQ (Angle opposite to larger side is larger) ... (1)
PS is the bisector of ∠QPR.
∴∠QPS = ∠RPS ... (2)
∠PSR is the exterior angle of ΔPQS.
∴ ∠PSR = ∠PQR + ∠QPS ... (3)
∠PSQ is the exterior angle of ΔPRS.
∴ ∠PSQ = ∠PRQ + ∠RPS ... (4)
Adding equations (1) and (2), we obtain
∠PQR + ∠QPS > ∠PRQ + ∠RPS
⇒ ∠PSR > ∠PSQ [Using the values of equations (3) and (4)]
APPEARS IN
संबंधित प्रश्न
Show that in a right angled triangle, the hypotenuse is the longest side.
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
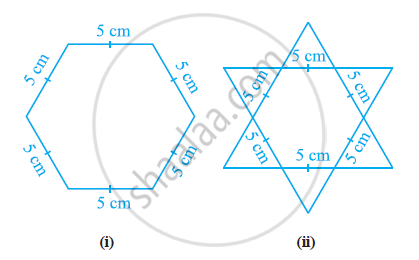
Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
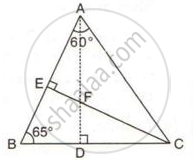
Prove that:
(i) CF > AF
(ii) DC > DF
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
