Advertisements
Advertisements
Question
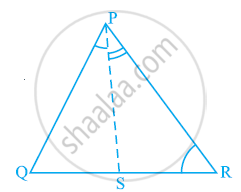
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
Solution
As PR > PQ,
∴ ∠PQR > ∠PRQ (Angle opposite to larger side is larger) ... (1)
PS is the bisector of ∠QPR.
∴∠QPS = ∠RPS ... (2)
∠PSR is the exterior angle of ΔPQS.
∴ ∠PSR = ∠PQR + ∠QPS ... (3)
∠PSQ is the exterior angle of ΔPRS.
∴ ∠PSQ = ∠PRQ + ∠RPS ... (4)
Adding equations (1) and (2), we obtain
∠PQR + ∠QPS > ∠PRQ + ∠RPS
⇒ ∠PSR > ∠PSQ [Using the values of equations (3) and (4)]
APPEARS IN
RELATED QUESTIONS
In a huge park people are concentrated at three points (see the given figure):

A: where there are different slides and swings for children,
B: near which a man-made lake is situated,
C: which is near to a large parking and exit.
Where should an ice-cream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlor should be equidistant from A, B and C)
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
"Caste inequalities are still prevalent in India." Examine the statement.
Arrange the sides of the following triangles in an ascending order:
ΔABC, ∠A = 45°, ∠B = 65°.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?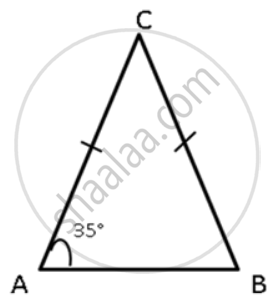
Prove that the perimeter of a triangle is greater than the sum of its three medians.
ABCD is a trapezium. Prove that: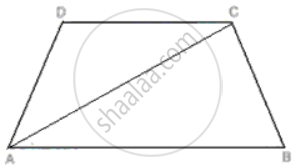
CD + DA + AB > BC.
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
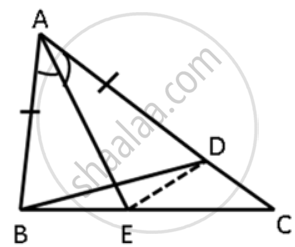
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.