Advertisements
Advertisements
Question
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Solution
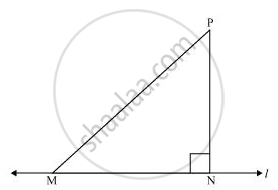
Let us take a line l and from point P (i.e., not on line l), draw two line segments PN and PM. Let PN be perpendicular to line l and PM is drawn at some other angle.
In ΔPNM,
∠N = 90º
∠P + ∠N + ∠M = 180º (Angle sum property of a triangle)
∠P + ∠M = 90º
Clearly, ∠M is an acute angle.
∴ ∠M < ∠N
⇒ PN < PM (Side opposite to the smaller angle is smaller)
Similarly, by drawing different line segments from P to l, it can be proved that PN is smaller in comparison to them.
Therefore, it can be observed that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
APPEARS IN
RELATED QUESTIONS
Show that in a right angled triangle, the hypotenuse is the longest side.
In the following figure, write BC, AC, and CD in ascending order of their lengths.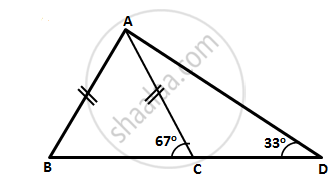
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.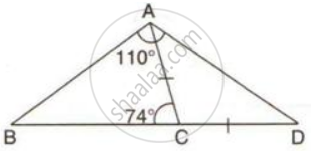
Prove that: BC > CD.
"Caste inequalities are still prevalent in India." Examine the statement.
"Issues of caste discrimination began to be written about in many printed tracts and essays in India in the late nineteenth century." Support the statement with two suitable examples.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
Prove that the hypotenuse is the longest side in a right-angled triangle.
ABCD is a trapezium. Prove that: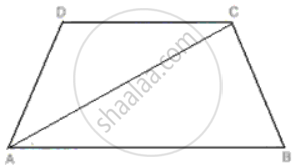
CD + DA + AB + BC > 2AC.
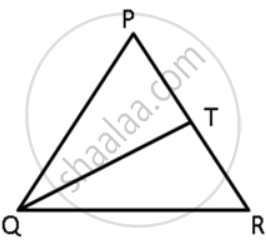
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT