Advertisements
Advertisements
Question
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
Solution
It is known that, in a triangle, the angle opposite to the smallest side is the smallest. In ΔPQR, QR = 5.4cm is the smallest side.
∴ ∠P is the smallest angle.
APPEARS IN
RELATED QUESTIONS
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
In the following figure, write BC, AC, and CD in ascending order of their lengths.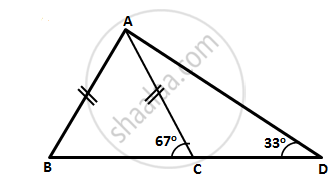
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.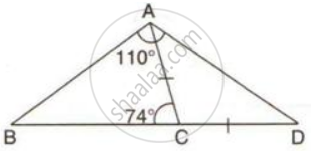
Prove that: BC > CD.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Arrange the sides of the following triangles in an ascending order:
ΔABC, ∠A = 45°, ∠B = 65°.
Prove that the perimeter of a triangle is greater than the sum of its three medians.
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).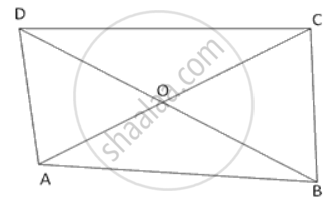
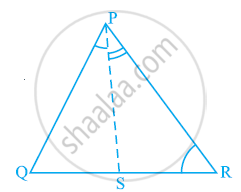
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR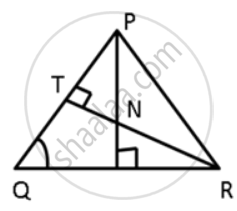
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.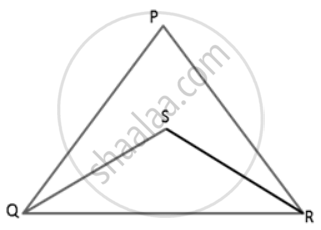
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
