Advertisements
Advertisements
Question
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.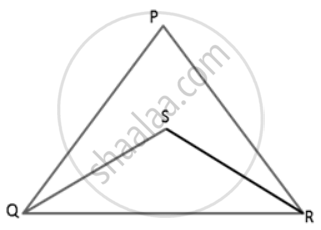
Solution
In ΔPQR,
PQ + PR > QR ....(∵ Sum of two sides of a triangle is always greater than the third side.) ....(i)
Also, in ΔSQR,
SQ + SR > QR ....(∵ Sum of two sides of a triangle is always greater than the third side.) ....(ii)
Dividing (i) by (ii),
`"PQ + PR"/"SQ + SR" > "QR"/"QR"`
`"PQ + PR"/"SQ + SR" > 1`
PQ + PR > SQ + SR
i.e. SQ + SR < PQ + PR.
APPEARS IN
RELATED QUESTIONS
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
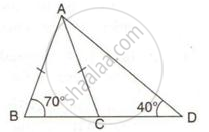
From the following figure, prove that: AB > CD.
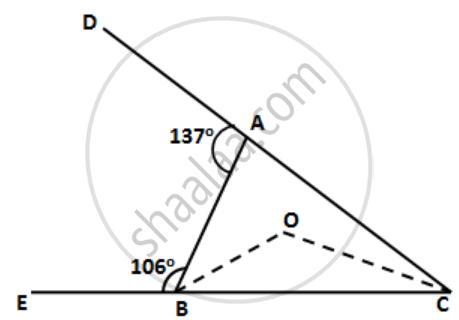
Arrange the sides of ∆BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Name the greatest and the smallest sides in the following triangles:
ΔXYZ, ∠X = 76°, ∠Y = 84°.
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.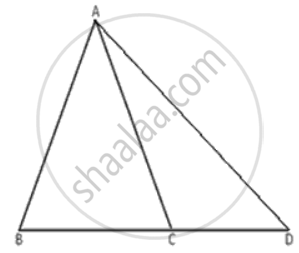
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT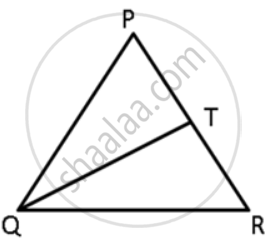
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.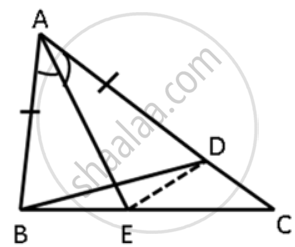
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
