Advertisements
Advertisements
प्रश्न
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.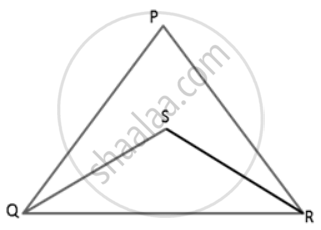
उत्तर
In ΔPQR,
PQ + PR > QR ....(∵ Sum of two sides of a triangle is always greater than the third side.) ....(i)
Also, in ΔSQR,
SQ + SR > QR ....(∵ Sum of two sides of a triangle is always greater than the third side.) ....(ii)
Dividing (i) by (ii),
`"PQ + PR"/"SQ + SR" > "QR"/"QR"`
`"PQ + PR"/"SQ + SR" > 1`
PQ + PR > SQ + SR
i.e. SQ + SR < PQ + PR.
APPEARS IN
संबंधित प्रश्न
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

From the following figure, prove that: AB > CD.
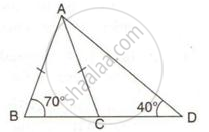
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
Prove that:
(i) CF > AF
(ii) DC > DF
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
Prove that the hypotenuse is the longest side in a right-angled triangle.
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
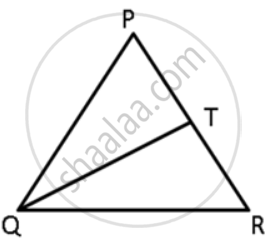
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.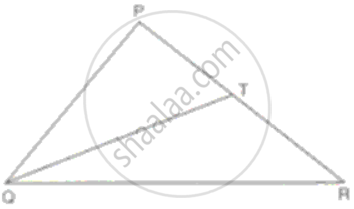
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT