Advertisements
Advertisements
Question
In ΔABC, AE is the bisector of ∠BAC. D is a point on AC such that AB = AD. Prove that BE = DE and ∠ABD > ∠C.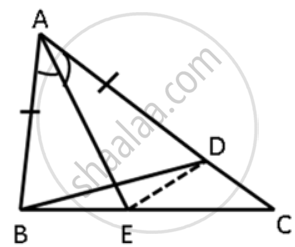
Solution
In the ΔABE and ΔADE,
AB = AD ....(Given)
∠BAE = ∠DAE ....(AE is the bisector of ∠BAC)
AE = AE ....(Common side)
∴ ΔABE ≅ ΔADE ....(SAS test)
⇒ BE = DE ....(c.p.c.t.c)
In ΔABD,
AB = AD
⇒ ∠ABD = ∠ADB
∠ADB > ∠C ...(Exterior angle property)
⇒ ∠ABD > ∠C.
APPEARS IN
RELATED QUESTIONS
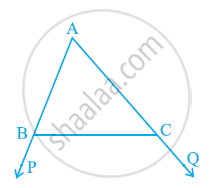
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
In the following figure, write BC, AC, and CD in ascending order of their lengths.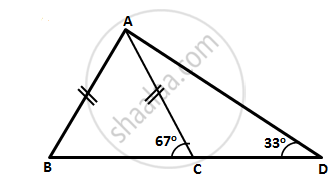
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
Prove that the hypotenuse is the longest side in a right-angled triangle.
ABCD is a trapezium. Prove that: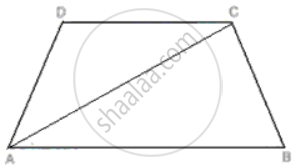
CD + DA + AB > BC.
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.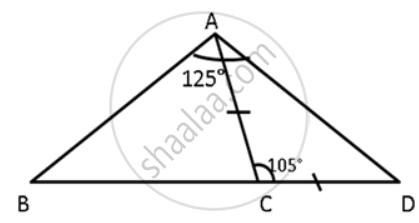
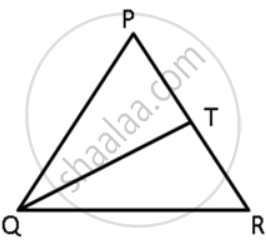
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT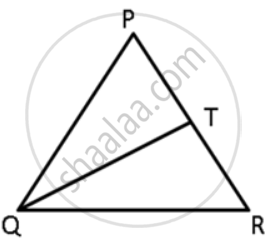
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT