Advertisements
Advertisements
Question
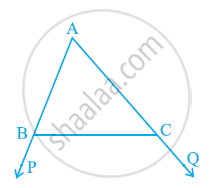
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
Solution
In the given figure,
∠ABC + ∠PBC = 180° (Linear pair)
⇒ ∠ABC = 180° − ∠PBC ... (1)
Also,
∠ACB + ∠QCB = 180°
∠ACB = 180° − ∠QCB … (2)
As ∠PBC < ∠QCB,
⇒ 180º − ∠PBC > 180º − ∠QCB
⇒ ∠ABC > ∠ACB [From equations (1) and (2)]
⇒ AC > AB (Side opposite to the larger angle is larger.)
APPEARS IN
RELATED QUESTIONS
Show that in a right angled triangle, the hypotenuse is the longest side.
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
In the following figure ; AC = CD; ∠BAD = 110o and ∠ACB = 74o.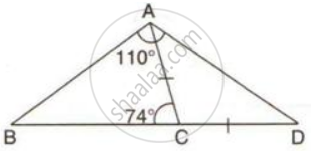
Prove that: BC > CD.
"Caste inequalities are still prevalent in India." Examine the statement.
Name the greatest and the smallest sides in the following triangles:
ΔXYZ, ∠X = 76°, ∠Y = 84°.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.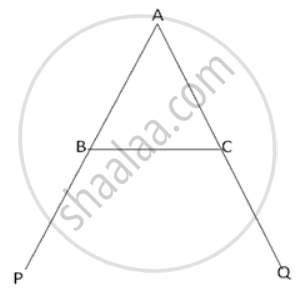
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
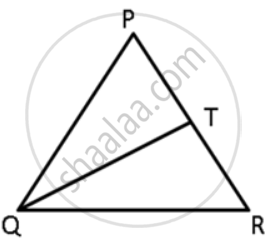
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.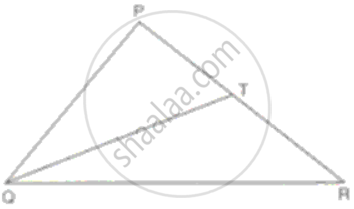
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that PT < QT