Advertisements
Advertisements
Question
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
Solution
In triangle APR,
AP + AR > PR ......(i)
In triangle BPQ,
BQ + PB > PQ .......(ii)
In triangle QCR,
QC + CR > QR .......(iii)
Adding (i), (ii) and (iii)
AP + AR + BQ + PB + QC + CR > PR + PQ + QR
(AP + PB) + (BQ + QC) + (CR + AR) > PR + QR + PQ)
⇒ AB + BC + AC > PQ + QR + PR.
APPEARS IN
RELATED QUESTIONS
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

In the following figure, write BC, AC, and CD in ascending order of their lengths.
Arrange the sides of the following triangles in an ascending order:
ΔABC, ∠A = 45°, ∠B = 65°.
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.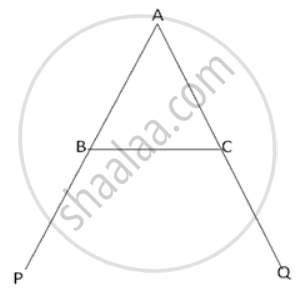
Prove that the perimeter of a triangle is greater than the sum of its three medians.
ABCD is a trapezium. Prove that: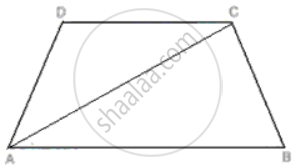
CD + DA + AB > BC.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR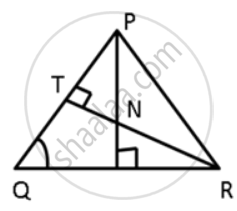
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS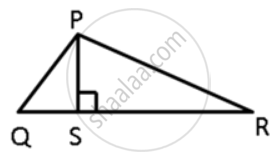
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.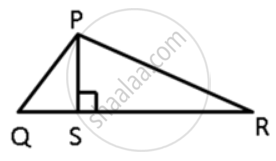
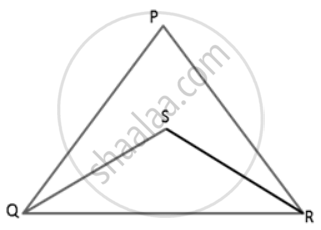
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.