Advertisements
Advertisements
Question
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.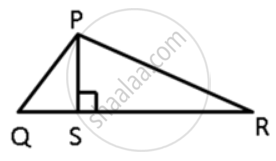
Solution
In ΔPQR,
PQ + PR > QR (∵ Sum of two sides of a triangle is always greater than third aside.)
In ΔPQS,
PQ + QS > PS (∵ Sum of two sides of a triangle is always greater than third aside.) .....(i)
In ΔPRS,
PR + SR > PS (∵ Sum of two sides of a triangle is always greater than third aside.) .....(ii)
Adding (i) and (ii),
PQ + QS + PR + SR > 2PS
PQ + (QS + SR) + PR > 2PS
PQ + QR + PR > 2PS
Since PQ + PR > QR
⇒ PQ + QR > 2PS.
APPEARS IN
RELATED QUESTIONS
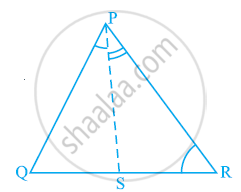
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
How had the position of women improved in our country since independence ? Explain with examples.
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Name the greatest and the smallest sides in the following triangles:
ΔXYZ, ∠X = 76°, ∠Y = 84°.
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
ABCD is a trapezium. Prove that: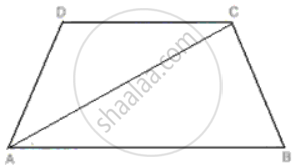
CD + DA + AB + BC > 2AC.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN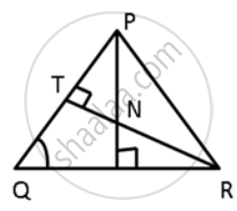
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.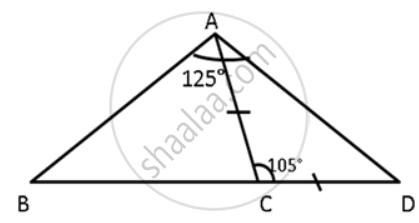
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
