Advertisements
Advertisements
Question
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN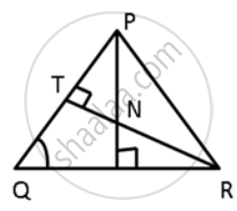
Solution
In the given ΔPQR,
PS < PR .....(Of all the straight lines that can be drawn to a given straight line from a point outside it, the perpendicular is the shortest)
PN < PR ....(i) (∵ PN < PS)
Also,
RT < PR .....(Of all the straight lines that can be drawn to a given straight line from a point outside it, the perpendicular is the shortest)
RN < PR .....(ii) (∵ RN < RT)
Dividing (i) bt (ii),
`"PN"/"RN" < "PR"/"PR"`
`"PN"/"RN" < 1`
PN < RN.
APPEARS IN
RELATED QUESTIONS
Show that in a right angled triangle, the hypotenuse is the longest side.
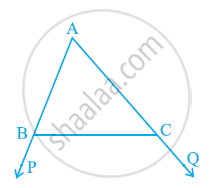
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
ABCD is a trapezium. Prove that: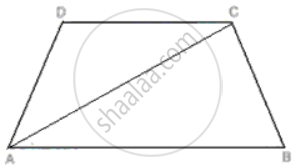
CD + DA + AB > BC.
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.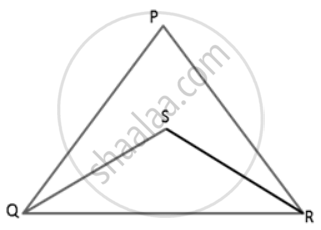
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
