Advertisements
Advertisements
Question
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
Solution
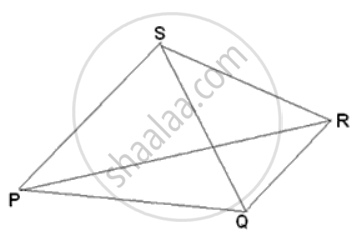
Given: PQRS is a quadrilateral.PR and QS are its diagonals.
To Prove: PQ + QR + SR + PS > PR + QS
Proof: In ΔPQR
PQ + QR > PR ...(Sum of two sides of triangle is greater than the third side)
Similarly, In ΔPSR, PS + SR > PR
In ΔPQS, PS + PQ > QS and in QRS we have QR + SR > QS
Now we have
PQ +QR > PR
PS + SR > PR
PS + PQ > QS
QR + SR > QS
After adding above inequalities we get
2(PQ + QR + PS + SR) > 2(PR + QS)
⇒ PQ + QR + PS + SR > PR +QS.
APPEARS IN
RELATED QUESTIONS
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
In the following figure, write BC, AC, and CD in ascending order of their lengths.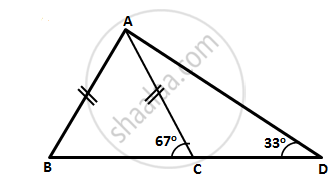
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
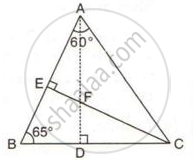
Prove that:
(i) CF > AF
(ii) DC > DF
In the following figure, write BC, AC, and CD in ascending order of their lengths.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.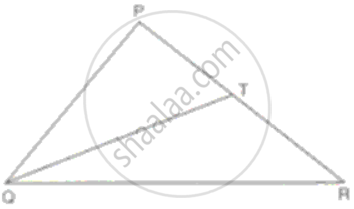
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.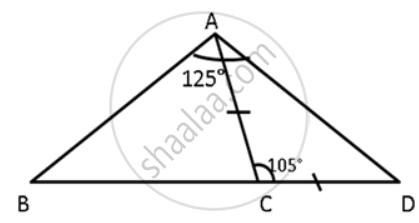
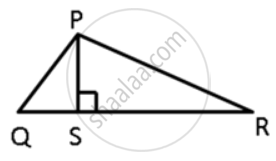
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS