Advertisements
Advertisements
Question
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
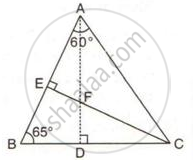
Prove that:
(i) CF > AF
(ii) DC > DF
Solution
In ΔBEC,
∠B + ∠BEC + ∠BCE = 180°
∠B = 65° ...[Given]
∠BEC = 90° ...[CE is perpendicular to AB]
⇒ 65° + 90° + ∠BCE = 180°
⇒ ∠BCE = 180° - 155°
⇒ ∠BCE = 25°= ∠DCF …(i)
In ΔCDF,
∠DCF + ∠FDC + ∠CFD = 180°
∠DCF = 25° ....[From (i)]
∠FDC = 90° ...[ AD is perpendicular to BC]
⇒ 25°+ 90°+ ∠CFD = 180°
⇒ ∠CFD = 180° - 115°
⇒ ∠CFD = 65° …(ii)
Now, ∠AFC + ∠CFD = 180° ....[AFD is a straight line]
⇒ ∠AFC + 65° = 180°
⇒ ∠AFC = 115° …(iii)
In ΔACE,
∠ACE + ∠CEA + ∠BAC = 180°
∠BAC = 60° ....[Given]
⇒ ∠CEA = 90° ...[CE is perpendicular to AB]
⇒ ∠ACE + 90° + 60° = 180°
⇒ ∠ACE = 180° - 150°
∠ACE = 30° …(iv)
In ΔAFC,
∠AFC + ∠ACF + ∠FAC = 180°
∠AFC = 115° ....[From (iii)]
∠ACF = 30° ...[From (iv)]
⇒ 115° + 30° + ∠FAC = 180°
⇒ ∠FAC = 180° - 145°
⇒ ∠FAC = 35° …(v)
In ΔAFC,
⇒ ∠FAC = 35° ...[ From (v) ]
⇒ ∠ACF = 30° ...[ From (iv) ]
∴ ∠FAC > ∠ACF
⇒ CF > AF
In Δ CDF,
∠DCF = 25° ...[From (i)]
∠CFD = 65° ...[From (ii)]
∴ ∠CFD > ∠DCF
⇒ DC > DF
APPEARS IN
RELATED QUESTIONS
Show that in a right angled triangle, the hypotenuse is the longest side.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.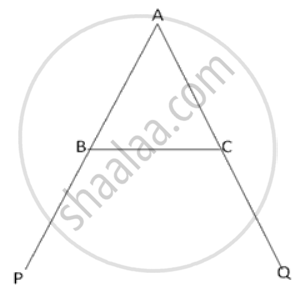
In ABC, P, Q and R are points on AB, BC and AC respectively. Prove that AB + BC + AC > PQ + QR + PR.
ABCD is a trapezium. Prove that: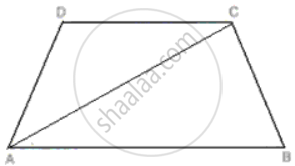
CD + DA + AB + BC > 2AC.
ABCD is a trapezium. Prove that: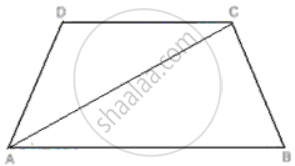
CD + DA + AB > BC.
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR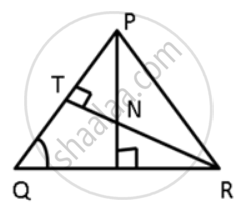
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS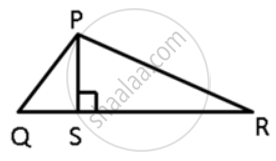
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT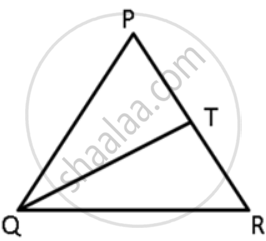
In ΔABC, D is a point in the interior of the triangle. Prove that DB + DC < AB + AC.
