Advertisements
Advertisements
Question
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.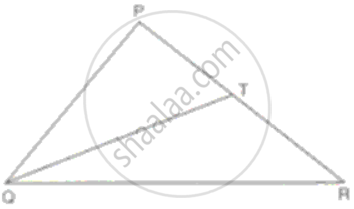
Solution
In ΔPQT, we have
PT = PQ ...(1)
In ΔPQR,
PQ + QR > PR
PQ + QR > PT + TR
PQ + QR > PQ + TR ...[Using (1)]
QR > TR
Hence, proved.
APPEARS IN
RELATED QUESTIONS
Show that in a right angled triangle, the hypotenuse is the longest side.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.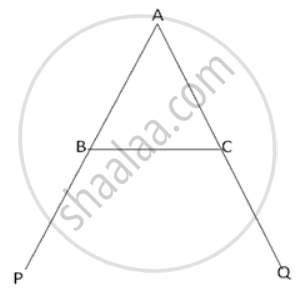
Prove that the hypotenuse is the longest side in a right-angled triangle.
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS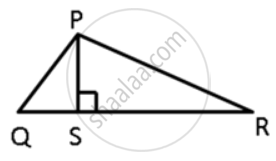
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.