Advertisements
Advertisements
प्रश्न
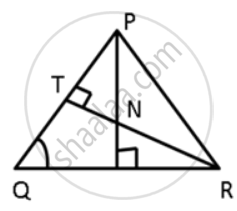
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.
उत्तर
In ΔPQT, we have
PT = PQ ...(1)
In ΔPQR,
PQ + QR > PR
PQ + QR > PT + TR
PQ + QR > PQ + TR ...[Using (1)]
QR > TR
Hence, proved.
APPEARS IN
संबंधित प्रश्न
Show that in a right angled triangle, the hypotenuse is the longest side.
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
Prove that the perimeter of a triangle is greater than the sum of its three medians.
Prove that the hypotenuse is the longest side in a right-angled triangle.
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).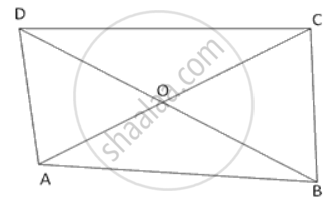
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR