Advertisements
Advertisements
प्रश्न
Prove that the hypotenuse is the longest side in a right-angled triangle.
उत्तर
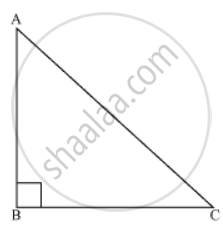
Let us consider a right angled triangle ABC, right angle at B.
In ΔABC
∠A + ∠B +∠C = 180° ...(angle sum property of a triangle)
∠A + 90° + ∠C = 180°
∠A +∠C = 90°
Hence, the other two angles have to be acute (i.e. less than 90°).
∴ ∠B is the largest angle in ΔABC.
⇒ ∠B > ∠A and ∠B > ∠C
⇒ AC > BC and AC > AB
[In ant triangle, the side opposite to the larger (greater) angle is longer]
So, Ac is the largest side in ΔABC.
But AC is the hypotenuse of ΔABC. Therefore, hypotenuse is the longest side in a right angled triangle.
APPEARS IN
संबंधित प्रश्न
In the following figure, write BC, AC, and CD in ascending order of their lengths.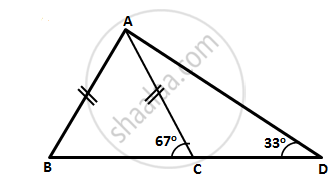
"Caste inequalities are still prevalent in India." Examine the statement.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the greatest and the smallest sides in the following triangles:
ΔXYZ, ∠X = 76°, ∠Y = 84°.
Name the smallest angle in each of these triangles:
In ΔPQR, PQ = 8.3cm, QR = 5.4cm and PR = 7.2cm
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.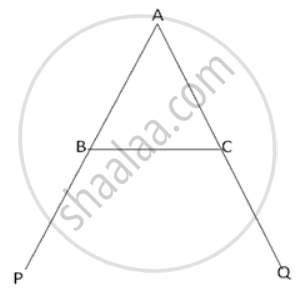
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).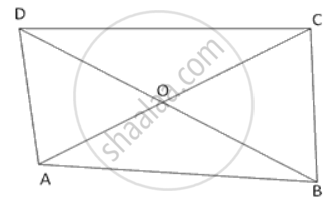
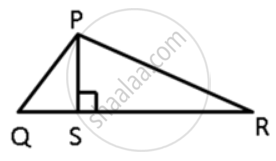
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS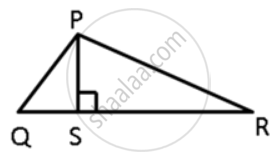
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.