Advertisements
Advertisements
प्रश्न
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).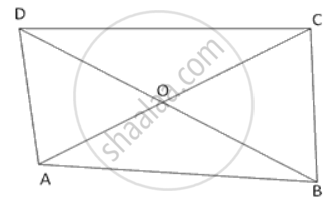
उत्तर
In ΔAOB, we have
OA + OB > AB ...(i)
In ΔBOC, we have
OB + OC > BC ...(ii)
In ΔCOD, we have
OC + OD > CD ...(iii)
In ΔAOD, we have
OA + OD > AD ....(iv)
Adding (i), (ii), (iii) and (iv), we get
2 (OA + OB + OC + OD) > AB + BC + CD + AD
⇒ 2 [(OA + OC) + (OB + OD)] > AB + BC + CD + AD
⇒ 2 (AC + BD) > AB + BC + CD + AD
[∵ OA + OC = AC and OB + OD = BD]
⇒ AB + BC + CD + AD < 2 (AC + BD).
APPEARS IN
संबंधित प्रश्न
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
How had the position of women improved in our country since independence ? Explain with examples.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the greatest and the smallest sides in the following triangles:
ΔXYZ, ∠X = 76°, ∠Y = 84°.
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.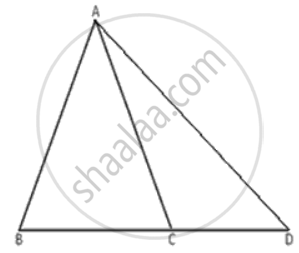
Prove that the perimeter of a triangle is greater than the sum of its three medians.
ABCD is a trapezium. Prove that: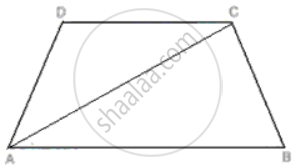
CD + DA + AB > BC.
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.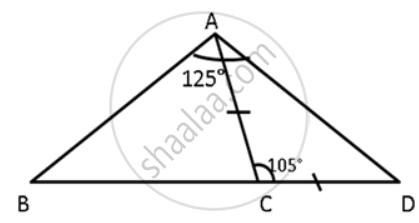
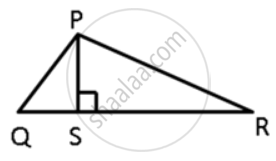
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS