Advertisements
Advertisements
प्रश्न
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
उत्तर
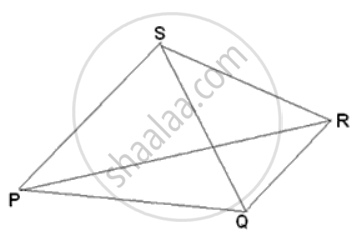
Given: PQRS is a quadrilateral.PR and QS are its diagonals.
To Prove: PQ + QR + SR + PS > PR + QS
Proof: In ΔPQR
PQ + QR > PR ...(Sum of two sides of triangle is greater than the third side)
Similarly, In ΔPSR, PS + SR > PR
In ΔPQS, PS + PQ > QS and in QRS we have QR + SR > QS
Now we have
PQ +QR > PR
PS + SR > PR
PS + PQ > QS
QR + SR > QS
After adding above inequalities we get
2(PQ + QR + PS + SR) > 2(PR + QS)
⇒ PQ + QR + PS + SR > PR +QS.
APPEARS IN
संबंधित प्रश्न
Show that in a right angled triangle, the hypotenuse is the longest side.
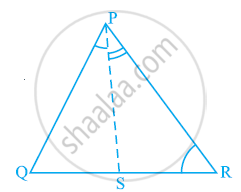
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Arrange the sides of the following triangles in an ascending order:
ΔABC, ∠A = 45°, ∠B = 65°.
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.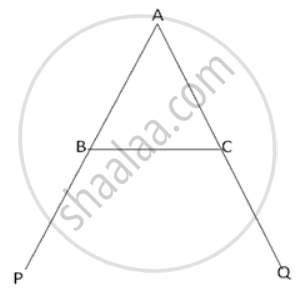
ABCD is a trapezium. Prove that: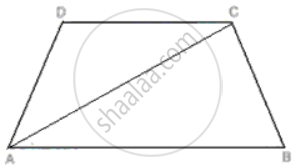
CD + DA + AB > BC.
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.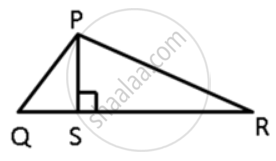
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT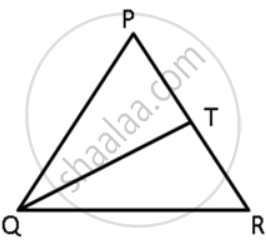
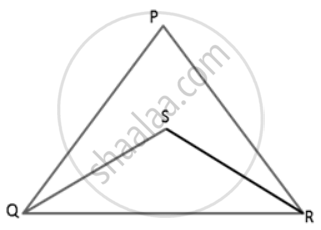
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.