Advertisements
Advertisements
प्रश्न
Show that in a right angled triangle, the hypotenuse is the longest side.
उत्तर
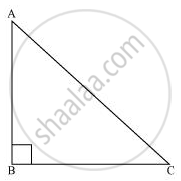
Let us consider a right-angled triangle ABC, right-angled at B.
In ΔABC,
∠A + ∠B + ∠C = 180° (Angle sum property of a triangle)
∠A + 90º + ∠C = 180°
∠A + ∠C = 90°
Hence, the other two angles have to be acute (i.e., less than 90º).
∴ ∠B is the largest angle in ΔABC.
⇒ ∠B > ∠A and ∠B > ∠C
⇒ AC > BC and AC > AB
[In any triangle, the side opposite to the larger (greater) angle is longer.]
Therefore, AC is the largest side in ΔABC.
However, AC is the hypotenuse of ΔABC. Therefore, hypotenuse is the longest side in a right-angled triangle.
APPEARS IN
संबंधित प्रश्न
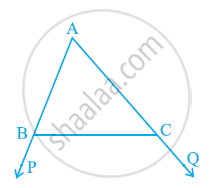
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

Complete the hexagonal and star shaped rangolies (see the given figures) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
In a triangle PQR; QR = PR and ∠P = 36o. Which is the largest side of the triangle?
"Caste inequalities are still prevalent in India." Examine the statement.
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.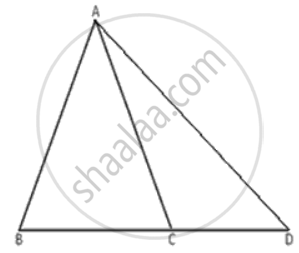
For any quadrilateral, prove that its perimeter is greater than the sum of its diagonals.
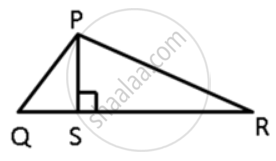
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PQ > PS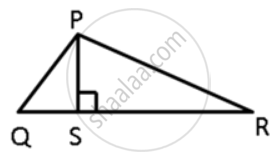
In ΔPQR, PS ⊥ QR ; prove that: PQ + PR > QR and PQ + QR >2PS.