Advertisements
Advertisements
प्रश्न
Arrange the sides of the following triangles in an ascending order:
ΔDEF, ∠D = 38°, ∠E = 58°.
उत्तर
In ΔDEF,
∠D + ∠E + ∠F = 180°
38° + 58° + ∠F = 180°
96° + ∠F = 180°
∠F = 180° - 96°
∠F = 84°
Hence, ∠D = 38°, ∠E = 58°, ∠F = 84°
38° < 58° < 84°
Hence, ascending order of the angles in the
given triangle is ∠D < ∠E < ∠F.
Hence, ascending order of sides in triangle
EF, DF, DE.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
Name the smallest angle in each of these triangles:
In ΔXYZ, XY = 6.2cm, XY = 6.8cm and YZ = 5cm
In ΔABC, the exterior ∠PBC > exterior ∠QCB. Prove that AB > AC.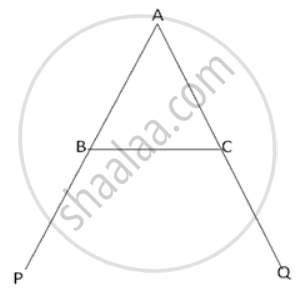
Prove that the perimeter of a triangle is greater than the sum of its three medians.
Prove that the hypotenuse is the longest side in a right-angled triangle.
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).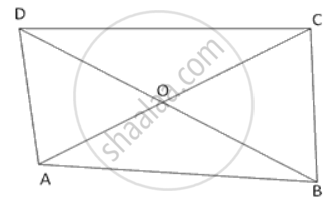
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that : PN < RN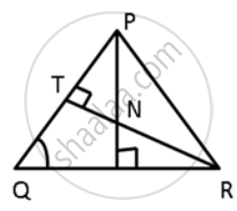
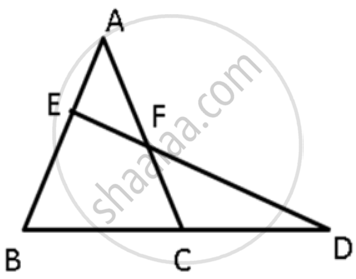
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.