Advertisements
Advertisements
प्रश्न
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
उत्तर
Circumcentre of a triangle is always equidistant from all the vertices of that triangle. Circumcentre is the point where perpendicular bisectors of all the sides of the triangle meet together.
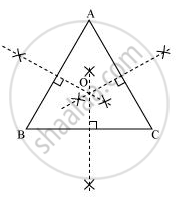
In ΔABC, we can find the circumcentre by drawing the perpendicular bisectors of sides AB, BC, and CA of this triangle. O is the point where these bisectors are meeting together. Therefore, O is the point which is equidistant from all the vertices of ΔABC.
APPEARS IN
संबंधित प्रश्न
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
If two sides of a triangle are 8 cm and 13 cm, then the length of the third side is between a cm and b cm. Find the values of a and b such that a is less than b.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
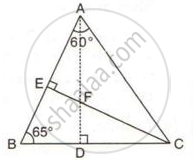
Prove that:
(i) CF > AF
(ii) DC > DF
Name the greatest and the smallest sides in the following triangles:
ΔXYZ, ∠X = 76°, ∠Y = 84°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.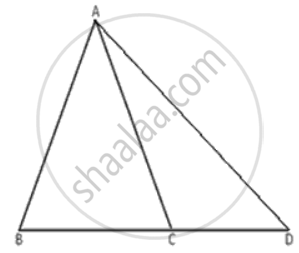
Prove that the perimeter of a triangle is greater than the sum of its three medians.
ABCD is a quadrilateral in which the diagonals AC and BD intersect at O. Prove that AB + BC + CD + AD < 2(AC + BC).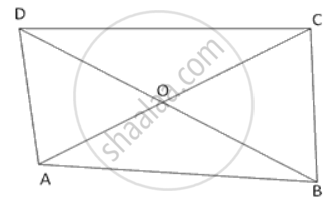
In the given figure, T is a point on the side PR of an equilateral triangle PQR. Show that RT < QT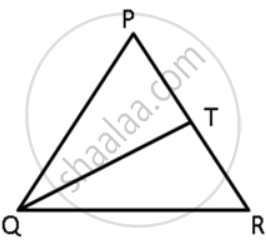
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
