Advertisements
Advertisements
प्रश्न
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.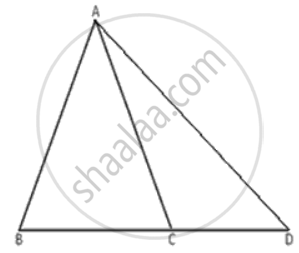
उत्तर
Using the exterior angle and property in ΔACD, we have
∠ACB = ∠CDA + ∠CAD
⇒ ∠ACB > ∠CDA ------(1)
Now, AB = AC
Now, ∠ACB = ∠ABC ------(2)
From (1) and (2)
∠ABC > ∠CDA
It is known that, in a triangle, the greater angle has the longer side opposite to it.
Now, In ΔABD, er have ∠ABC > ∠CDA
∴ AD > AB.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
"Issues of caste discrimination began to be written about in many printed tracts and essays in India in the late nineteenth century." Support the statement with two suitable examples.
Name the greatest and the smallest sides in the following triangles:
ΔABC, ∠ = 56°, ∠B = 64° and ∠C = 60°.
Name the smallest angle in each of these triangles:
In ΔABC, AB = 6.2cm, BC = 5.6cm and AC = 4.2cm
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?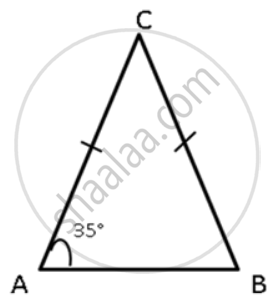
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In ΔPQR, PR > PQ and T is a point on PR such that PT = PQ. Prove that QR > TR.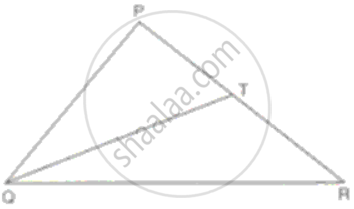
In the given figure, ∠QPR = 50° and ∠PQR = 60°. Show that: SN < SR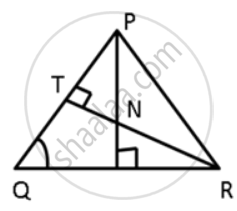
In ΔABC, BC produced to D, such that, AC = CD; ∠BAD = 125° and ∠ACD = 105°. Show that BC > CD.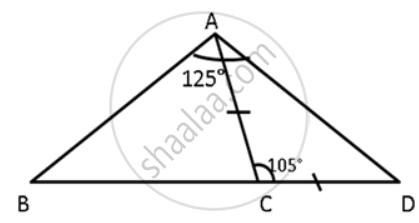
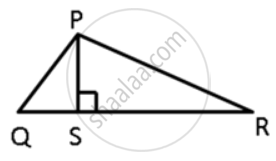
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS