Advertisements
Advertisements
प्रश्न
In a triangle ABC, BC = AC and ∠ A = 35°. Which is the smallest side of the triangle?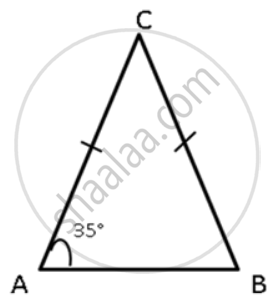
उत्तर
In ΔABC,
BC = AC ...(given)
⇒ ∠A = ∠B = 35°
Let ∠C = x°
In ΔABC,
∠A + ∠B + ∠C = 180°
35° + 35° + x = 180°
70° + x° = 180°
x° = 180° - 70°
x° = 110°
∠C = x° = 110°
Hence, ∠A = ∠B = 35° and ∠C = 110°
In ΔABC, the greatest angle is ∠C.
As the smallest angles are ∠A and ∠B,
smallest sides are BC and AC.
APPEARS IN
संबंधित प्रश्न
Show that in a right angled triangle, the hypotenuse is the longest side.
D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.
In the following figure, ∠BAC = 60o and ∠ABC = 65o.
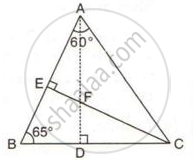
Prove that:
(i) CF > AF
(ii) DC > DF
Name the greatest and the smallest sides in the following triangles:
ΔDEF, ∠D = 32°, ∠E = 56° and ∠F = 92°.
ΔABC is isosceles with AB = AC. If BC is extended to D, then prove that AD > AB.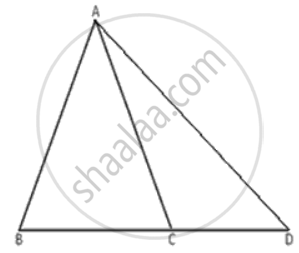
D is a point on the side of the BC of ΔABC. Prove that the perimeter of ΔABC is greater than twice of AD.
In ΔPQR, PS ⊥ QR ; prove that: PQ > QS and PR > PS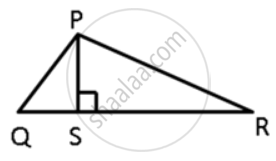
In ΔPQR is a triangle and S is any point in its interior. Prove that SQ + SR < PQ + PR.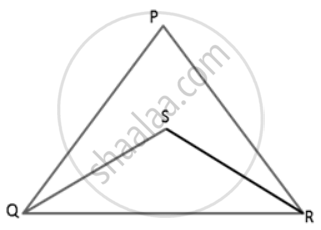
Prove that in an isosceles triangle any of its equal sides is greater than the straight line joining the vertex to any point on the base of the triangle.
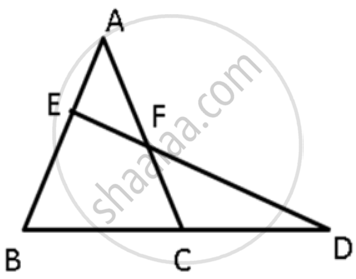
ΔABC in a isosceles triangle with AB = AC. D is a point on BC produced. ED intersects AB at E and AC at F. Prove that AF > AE.